ТРАЕКТОРИИ, УПРАВЛЕНИЕ, НАВИГАЦИЯ,
РАДИОСВЯЗЬ, АВАРИЙНОЕ ВОЗВРАЩЕНИЕ
3.1. ПРИЦЕЛИВАНИЕ ТРАЕКТОРИИ ПОЛЕТА
ЗЕМЛЯ-ЛУНА-ЗЕМЛЯ
Задача прицеливания на траектории выведения к Луне состоит в определении параметров старта с Земли и участка разгона с околоземной орбиты (независимые переменные) для заданного набора параметров прицеливания (зависимые переменные). Параметрами прицеливания являются радиус периселения окололунной траектории Rm, ширина периселения в лунной системе координат Lm и высота условного перицентра траектории возвращения RE. В качестве трех независимых переменных рассматриваются время старта Tl, продолжительность движения на промежуточной околоземной орбите tc и удельная энергия на траектории к Луне С3. Эти переменные, будучи определенными с помощью итеративного процесса, устанавливают 3 важных зависимых параметра задачи: время старта для заданного азимута, время до второго включения ступени S-IVB при разгоне с околоземной орбиты (на втором или третьем обороте) и удвоенную удельную энергию эллиптической траектории полета к Луне.
При вычислении независимых переменных используется метод Ньютона-Рафсона для системы нелинейных уравнений. Линеаризованные уравнения, записанные в матричной форме, имеют следующий вид:
Для заданного азимута запуска траектория выведения на орбиту ИСЗ оптимизируется независимо от расположения Земли и Луны. Однако участок разгона с орбиты зависит от расположения Земли и Луны, которое определяет требования к изменению плоскости движения при втором запуске ступени S-IVB. Поэтому участок выведения на траекторию полета к Луне должен оптимизироваться совместно с определением независимых переменных. Схема, выбранная для вычислительной программы прицеливания ракеты-носителя на участке выведения к Луне, основана на аппроксимации по методу наименьших квадратов оптимальных параметров активного участка полета ступени S-IVB, выражаемых через параметры гиперповерхности. Это позволяет независимо оптимизировать выведение на траекторию полета к Луне в процессе итерационного вычисления зависимых переменных. Гиперповерхность, показанная на рис. 31.1, образована путем состыковки конических сечений для двух притягивающих центров.

Рис. 31.1. Гиперповерхность траекторий полета к Луне
Она представляет собой семейство конических сечений, которые начинаются у Земли и заканчиваются вблизи сферы действия Луны. Гиперповерхность определяют следующие параметры: вектор цели Т°, удвоенная удельная энергия С3, угол между вектором цели и радиусом-вектором перигея s.

Рис. 31.2. Параметры участка выведения на траекторию полета к Луне:
а—вид в плоскости выведения; б—проекция на плоскость, перпендикулярную плоскости выведения
Параметры гиперповерхности используются в качестве независимых переменных полиномов, описывающих активный участок ступени S-IVB. С помощью этих полиномов определяются параметры участка выведения к Луне и вектора состояния. На рис. 31.2 показаны участок выведения и геометрические соотношения для определения гиперповерхности.
При использовании полиномов необходимо знать удельную энергию на траектории к Луне С3, угол между вектором цели и радиусом-вектором перигея s, а также склонение вектора цели относительно плоскости промежуточной орбиты d. С помощью полиномов вычисляются параметры: a—угол между радиусом-вектором точки начала выведения и проекцией вектора цели на плоскость промежуточной орбиты (Т'); b—угол между радиусом-вектором точки начала выведения и узлом орбиты (W); h—истинная аномалия радиуса-вектора точки конца выведения; Rp — радиус перигея участка выведения к Луне. Параметры a, w, h и Rp задают вектор состояния участка выведения.
В системе уравнений указанные величины используются для определения параметров активного участка и вычисления переменных, соответствующих моменту выключения двигателя. По полиномам также вычисляется приращение характеристикой скорости DV при повторном включении ступени S-IVB. Величина этого приращения необходима для определения веса аппарата и времени работы двигателя. Из-за неточности учета влияния сжатия Земли и модели изменения тяги расчеты по полиномам не совпадают с результатами оптимизации активного участка методом вариационного исчисления на основе ожидаемых параметров отлета от Земли. Поэтому полиномы тарируются, чтобы обеспечить данные, точно совпадающие с результатами расчета активного участка методом вариационного исчисления. Постоянные поправочные члены, необходимые для тарировки, вычисляются как разница между результатами расчета методом вариационного исчисления и величинами, полученными путем оценки полиномов в первом приближении при С3=С3g (где C3g—приближенное значение), d=0 (компланарный случай) и d=6°:

В компланарном случае b=a+s и Da=Db. Указанные поправочные члены получены для обеих возможностей запуска и должны использоваться всякий раз, когда параметры активного участка вычисляются по аппроксимирующим полиномам. Полиномы для участка выведения к Луне тарируются путем добавления вычисленных поправочных членов к приближенным величинам, полученным при подстановке в полиномы текущих величин С3, d и s.
Полином, определяющий величину DV при втором включении ступени S-IVB, не тарируется. Однако при каждом расчете по полиному вычисляется разница между компланарным значением DV, основанным на параметрах первого приближения (C3g, d=0, s=6°), и значением DV, определяемым текущими величинами указанных параметров:
Логика выбора времени запуска
При планировании задачи полета на Луну определенное преимущество достигается в случае двух возможностей отлета с околоземной орбиты. Вторая возможность появляется приблизительно через 90 мин после первой (т. е. через один оборот на промежуточной орбите ИСЗ) и оказывается полезной в тех случаях, когда не все системы ракеты-носителя и космического корабля проверены и готовы к повторному включению двигателя для выведения на траекторию полета к Луне. В процессе подготовки полета принимается решение о том, сохранять ли время перелета к Луне для второй возможности таким же, какое требовалось для первой (класс 1) или уменьшить время полета для второй возможности на 90 мин (класс 2). Уменьшение времени перелета на 90 мин при использовании второй возможности позволяет сохранить время прибытия к Луне приблизительно таким же, как для первой возможности.

Рис. 31.3. Выбор компромиссного времени старта:
1—первая возможность; 2—вторая возможность; 3—компромиссное время старта; 4—моменты времени, соответствующие компланарному выведению
В процессе прицеливания ракеты-носителя и выбора времени запуска исследуются оба класса перелетов с целью получения максимального веса на траектории к Луне для обеих возможностей запуска. Рис. 31.3 иллюстрирует логику выбора времени запуска для двух рассматриваемых классов.
Вектор цели для компланарной траектории расположен в плоскости второго активного участка (т. е. d=0), и в процессе выведения к Луне никакого изменения плоскости движения не совершается. Это справедливо для обеих возможностей запуска при компланарных траекториях перелета. Однако, пока ракета-носитель и космический корабль находятся на промежуточной орбите в ожидании второй возможности старта, Луна продолжает двигаться по орбите вокруг Земли в течение дополнительных 90 мин, что приводит к изменению вектора цели. На рис. 31.4 показано перемещение вектора цели,

Рис. 31.4. Компромиссная траектория выведения
обусловленное движением Луны, от первой до второй возможности запуска, а также соответствующие моменты старта. Если рассматриваются 2 возможности выведения к Луне, то следует определить общее компромиссное время запуска. По крайней мере для одной из возможностей потребуется выполнить маневр по изменению плоскости движения, так как общее время запуска может удовлетворять условию d=0 только для одной возможности. На рис. 31.3 показано изменение веса на траектории к Луне и времени запуска для обеих возможностей выведения. Максимальный вес обеспечивается, когда время запуска соответствует компланарному перелету, однако при второй возможности перелета вес оказывается меньше, чем при первой вследствие дренажа газообразного водорода из бака в течение дополнительного оборота на промежуточной орбите. Как видно из графиков, представленных на рис. 31.3, существует только одно время запуска, которое позволяет получить одинаковый вес на траектории к Луне для обеих возможностей. В случае а точка одинакового веса (точка пересечения кривых) расположена между временами двух компланарных запусков. Время запуска, позволяющее получить одинаковую полезную нагрузку, является общим для обеих возможностей и называется здесь компромиссным временем. В случае б точка пересечения двух кривых расположена правее времени компланарного запуска для второй возможности. Это имеет место, когда время между первой и второй возможностями оптимального запуска (DTL) мало. В случае б оптимальным решением для обеих возможностей запуска является время, соответствующее второму компланарному запуску. Процедура выбора компромиссного времени запуска состоит в следующем:
1) рассчитывается траектория для второй возможности компланарного запуска; 2) вычисляется вектор цели для первой возможности компланарного запуска; 3) определяется DTL; 4) находится компромиссное время запуска, основанное на векторах цели для первой и второй возможностей компланарного запуска.
Отвечающее требованиям прицеливания приближенное значение вектора цели для первой возможности запуска (шаг 2 процедуры) можно вычислить без интегрирования траектории.

Рис. 31.5. К расчету времени старта для первой возможности.
При этом с помощью системы координат, связанной с плоскостью движения Луны (рис. 31.5), предварительно устанавливается соотношение между вектором цели для второй возможности запуска Т02 и положением линии Луна-Земля в момент, соответствующий прибытию в периселений. Методика вычислений состоит в следующем. Даны величины: R0ME2—единичный вектор, направленный по линии Луна-Землд в момент прибытия в периселений по компланарной траектории, соответствующей второй возможности запуска и использованию времени для второй компланарной траектории; Т02—вектор цели для второй возможности компланарного запуска; N0m—единичный вектор, перпендикулярный плоскости движения Луны. Рассмотрим следующие уравнения:
jm=arcsin(N0m·Т02);
Т02'=Т02-N0msinjm/cosjm
qm=arcsin(q02·Т02'),
где qm—единичный вектор, дополняющий N0m и R0ME2 до правой ортогональной системы координат,: jm — склонение вектора цели Т02 относительно плоскости движения; Т02—проекция вектора цели на плоскость движения Луны; qm—прямое восхождение вектора Т02, измеряемое в плоскости движения Луны от линии Луна-Земля, соответствующей моменту прибытия в периселений по второй возможной компланарной траектории.
Предполагается, что вектор цели остается на постоянных угловых расстояниях jm и qm от линии Луна-Земля. Если выведение к Луне происходит при первой возможности, а запуск имеет место во время, соответствующее второй возможной компланарной траектории, то положение линии Луна-Земля в момент прибытия в периселений определяется посредством выбора эфемериды, которая сдвинута назад относительно момента прибытия на один период обращения по промежуточной орбите. Вектор цели вычисляется на угловых расстояниях jm и qm от результирующего положения линии Луна-Земля, как показано на рис. 31.5. Кроме того отыскивается вектор цели, соответствующий времени первого возможного компланарного запуска, причем должно учитываться дополнительное влияние DTL. В первом приближении вектор цели Т02' вычисляется без учета влияния DTL:
y=arcsin(R0ME2·R0ME1);(31.5)
Т01'=[R0ME2, q02, N0m] X [0195 (31.6)
где ф—угол между векторами R0ME2 и R0ME1;

Склонение и прямое восхождение Т01 определяется как
RAS1=arctg(T'1y/T'1x)+2p.
При вычислении вектора цели Т01 будем рассматривать его в качестве функции от DTL с тем, чтобы можно было применить итерационную процедуру для обеспечения перпендикулярности вектора цели Т01 и нормали к плоскости промежуточной орбиты в случае первой возможности запуска N01 , т. е. совпадения плоскости перелета и промежуточной орбиты. Из уравнения (31.6) при DTL=0 в первом приближении определяется вектор цели для первой возможности компланарного запуска. Принимая линейную зависимость прямого восхождения и склонения от DTL, можно получить уравнения для вычисления этих углов по следующим формулам:
 (31.7)
(31.7)Остальные уравнения, используемые в итерационной процедуре, представлены ниже

tE=wEDTL-R
R=2pJ(RE/Rp0)2N2z;
Величины для определения производной дd/дDTL вычисляются путем решения уравнений (31.7)—(31.10) при DTL=0 и 60 сек. При вычислении дd/дDTL принимается линейное соотношение между d и DTL. Уравнения (31.7) и (31.10) образуют итерационный контур, из которого можно определить величину DTL удовлетворяющую условию d=0. Когда условие d=0 выполнено, текущее значение DTL представляет собой время между моментами компланарных запусков для двух возможностей, как показано на рис. 31.3 (в случаях а и б). Текущее значение Т01 является вектором цели для первой возможности компланарного запуска. Когда необходимо, эти величины затем используются при определении компромиссного времени запуска.
Зависимости параметров активного участка в виде полиномов используются при вычислении веса в конце участка выведения к Луне для первой возможности запуска, осуществляемого в момент времени, соответствующий второй возможности компланарного запуска. Для вектора Т01 вычисляется угол наклона d к плоскости промежуточной орбиты, а значения С3 и s приравниваются к величинам, полученным из исследования второй возможности компланарного запуска и гиперповерхности. Результирующий вес W1 сравнивается с полученным ранее весом для второй возможности компланарного запуска W2. Если W1+23 Kг ≤W2, то в качестве общего времени запуска используется время, соответствующее второй возможности компланарного запуска. Если же W1+23кг<W2, то вычисляется компромиссное время запуска.
Для определения компромиссного времени запуска применяется метод последовательных приближений. При этом производится варьирование ориентации плоскости промежуточной орбиты в инерциальном пространстве между векторами Т01 и Т02 таким образом, чтобы изменение плоскости движения приводило к получению одинакового веса в конце участка выведения для обеих возможностей запуска. Требуемая ориентация плоскости промежуточной орбиты соответствует компромиссному времени запуска и достигается путем варьирования N01 и N02 от исходных положений. Вектор N02 варьируется посредством уменьшения времени запуска на величину DTs (измеряемую от времени второй возможности компланарного запуска), а вектор N01—путем увеличения времени запуска соответственно на DTL—DTs-Величина DTsизменяется до тех пор, пока веса в конце участков выведения для первой и второй возможностей запуска не станут равными. Для получения компромиссного времени запуска текущая величияа DTs вычитается затем из времени соответствующего второй возможности компланарного запуска.
Ошибка при определении компромиссного времени запуска описанным выше способом может достигать ~20 сек. Однако это время отвечает требованиям проведения итерационных расчетов, связанных с изменением плоскости движения при первой и второй возможностях запуска. После проведения этих расчетов полученные векторы цели, которые принадлежат гиперповерхности, соответствующей изменению плоскости движения, используются для расчета второго приближения компромиссного времени запуска. Нормальные к плоскости промежуточной орбиты векторы снова варьируются, чтобы уравнять веса на траектории полета к Луне. Использование скорректированного компромиссного времени запуска в программе моделирования активного участка показало достаточную точность процедуры уравнивания весов. Это приводило к незначительному расходу топлива на коррекцию среднего участка траектории, связанную с использованием времени запуска, отличающегося от запланированного.
Как следует из рис. 31.3, время запуска для задачи, относящейся к классу 2, определяется существенно проще. Времена запуска для первой и второй возможностей в случае в (рис. 31.3) не являются одинаковыми из-за прецессии орбиты к моменту наступления второй возможности старта. Однако это влияние незначительно и не затрагивает логики, которая используется при выборе траекторий класса 2. Анализ параметров прицеливания показывает, какой класс траекторий (1 или 2) должен использоваться. Когда установлено, что имеет место случай в, то участки вычислительной программы для случаев а и б обходятся. Вектор цели для второй возможности запуска и соответствующие параметры (гиперповерхность) вычисляются на основе времени старта при компланарном перелете. Время запуска для второй возможности используется при определении параметров прицеливания для первой возможности. Как указывалось выше, это время запуска не будет являться оптимальным для первой возможности, однако оно отличается от оптимального всего на несколько секунд.
Как отмечалось выше, лунными параметрами прицеливания (т. е. зависимыми переменными в схеме вычислений) являются радиус максимального сближения Rm и широта j* в селеноцентрической системе координат. Однако эти переменные являются нелинейными по отношению к изменению независимых переменных. Определение широты j* представляет собой особую проблему, потому что в селеноцентрической системе координат эта задача двузначна (одной и той же широты можно достигнуть при сближении по направлению движения Луны и против направления движения). Для получения эффективной вычислительной схемы используются метод параметров попадания и метод перемещающейся конечной точки. Система координат для параметров попадания при встрече с Луной строится, как показано на рис. 31.6; ось Т0m находится в плоскости лунного экватора,
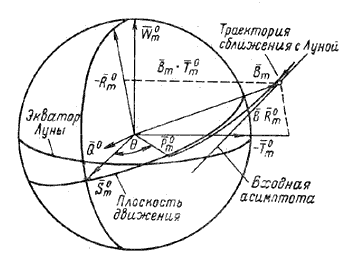
Рис. 31.6. Параметры попадания при встрече с Луной.
ось S0m параллельна входной асимптоте и расположена в плоскости движения, а ось R0m дополняет систему до правой. Параметры попадания В.Т0 и B.R 0 для заданных значений Rm и наклонения Ist
 где Т
0, R0 — единичные векторы; звездочка означает требуемые конечные условия; а — большая полуось гиперболы. Как видно из рис. 31.7, траектория первого приближения достаточно точно определяет величину а. Даже когда траектория первого приближения не будет удовлетворять заданным конечным условиям, например, не достигается величина Rm*, тем не менее входная асимптота и большая полуось окажутся близкими к заданным конечным величинам. Это медленное изменение асимптоты можно классифицировать как квазипостоянство входной асимптоты гиперболической траектории. Однако параметры прицеливания содержат широту j* вместо наклонения Ist*. Основываясь на принципе квазипостоянства входной асимптоты гиперболической траектории,
где Т
0, R0 — единичные векторы; звездочка означает требуемые конечные условия; а — большая полуось гиперболы. Как видно из рис. 31.7, траектория первого приближения достаточно точно определяет величину а. Даже когда траектория первого приближения не будет удовлетворять заданным конечным условиям, например, не достигается величина Rm*, тем не менее входная асимптота и большая полуось окажутся близкими к заданным конечным величинам. Это медленное изменение асимптоты можно классифицировать как квазипостоянство входной асимптоты гиперболической траектории. Однако параметры прицеливания содержат широту j* вместо наклонения Ist*. Основываясь на принципе квазипостоянства входной асимптоты гиперболической траектории,
Рис. 31.7. Определение переменных для расчета параметров попадания при встрече с Луной.
можно вычислить приблизительно требуемый угол Q* между асимптотой и радиусом-вектором перицентра. Зная асимптоту, т. е. вектор Sm* после первого приближения, а также требуемые величиныQ*, Rm* и j*, можно из геометрических соотношений представить R*m и j* через (В.Т 0)* и (B.R0)*. Для этого рассмотрим следующие уравнения (рис. 31.6):
 где Wm0—единичный вектор угловой скорости вращения Луны; q*—угол между входной асимптомой гиперболы и заданным радиусом-вектором периселения; a'—угол между Wm0 и Sm0; b'—угол между Wш0 и заданным радиусом-вектором периселения; Ist* — угол между Tm0 и В*m .
где Wm0—единичный вектор угловой скорости вращения Луны; q*—угол между входной асимптомой гиперболы и заданным радиусом-вектором периселения; a'—угол между Wm0 и Sm0; b'—угол между Wш0 и заданным радиусом-вектором периселения; Ist* — угол между Tm0 и В*m .
Так как первые вычисленные значения величин (В·Т0)* и (B-R
0)* не являются заданными, используется принцип ограничения перемещения конечной точки. Вследствие изменения входной асимптоты гиперболы изменяются также величины q* и а. Результатом этого является медленное изменение (В·Т0)* в процессе вычислений, однако процесс быстро сходится, так что заданные величины Rm* и j* и получаются эффективно.
Для вычисления параметров точки попадания используются формулы

Q0—единичный вектор скорости в периселении; Вm вектор, направленный из центра Луны перпендикулярно входной асимптоте.
Действительные лунные параметры попадания определяются как

Земные параметры попадания
Радиус наибольшего сближения с Землей RЕ также выражается через параметры попадания, чтобы гарантировать монотонность и достаточную линейность функций относительно переменных отправления от Земли. На рис. 31.8 показаны траектория возвращения к Земле и система координат для определения параметров попадания. Вектор S0E направлен приблизительно вдоль линии Луна-Земля, соответствующей моменту отправления от луны, Т0Е расположен в плоскости земного экватора, R0E дополняет систему до правой
На рис. 31.9 показаны зависимости BЕ·Т0Е и BЕ·R0Е от продолжительности активного участка ступени S=IVB и времени старта для тех же условий отправления от Земли.
Поскольку вблизи Земли ограничен лишь параметр RE,-необходима только одна компонента параметра попадания. Вычисления показывают, что при изменении каждого из

Рис. 31.8. Параметры попадания при встрече с Землей.

Рис. 31.9. Зависимость параметров попадания и re от изменения продолжительности активного участка и времени старта.
трех начальных условий величина BЕ·T0Е изменяется сильнее, чем BЕ·R0Е. При определении параметра (BЕ·T0Е)* через RE* вычисления производятся по следующим формулам:

где bE*—заданная величина эллиптического параметра попадания; I*stE—заданный угол между В0E и T0E; В·T0E—заданный параметр попадания при возвращении к Земле.
Вычисление действительных величин В·T0E и В·R0E в процессе каждой итерации производится следующим образом. В перигее заданы радиус-вектор относительно центра Земли R, вектор скорости V и большая полуось геоцентрического эллипса а. Расчет проводится по формулам
 где Np0—единичный вектор, перпендикулярный плоскости геоцентрического эллипса; f—угол между R
0 и ВE0; е—эксцентриситет геоцентрического эллипса; bE—модуль вектора B0E, направленного перпендикулярно S0E из центра Земли к действительной входной траектории; ВE, TE0, ВE, RE0—действительные параметры попадания.
где Np0—единичный вектор, перпендикулярный плоскости геоцентрического эллипса; f—угол между R
0 и ВE0; е—эксцентриситет геоцентрического эллипса; bE—модуль вектора B0E, направленного перпендикулярно S0E из центра Земли к действительной входной траектории; ВE, TE0, ВE, RE0—действительные параметры попадания.
Траектории, которые подходят к Луне по направлению движения, не гарантируют получения участка возвращения к Земле, который будет отвечать требованиям сходимости процесса расчета траекторий. Чтобы обеспечить получение траектории возвращения к Земле, в схеме расчета с использованием сфер действия вводится разрыв между окололунным и околоземным участками траектории. На каждой окололунной траектории согласно рассматриваемой схеме расчета космический корабль переводится из состояния, соответствующего действительному периселению, в требуемое состояние. После этого начинается интегрирование околоземной траектории. Разрыв исчезает при достижении сходимости. Показанные на рис. 31.7 геометрические соотношения для окололунного участка позволяют определить Rm* и jm*. Если известны вектор Sm0 и наклонение Ist*, то требуемые значения радиуса-вектора периселения Р* и вектора скорости Q* можно вычислить по следующим формулам:

назад