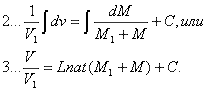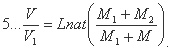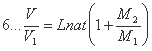вернёмся в библиотеку?

Перевод на современный
на дореволюционном

---

Дозволено цензурою СПБ. 31 мая 1903 года.

---

СОДЕРЖАНИЕ № 5.

---

ОТДЕЛ ПЕРВЫЙ.
1. Заветныя мысли. Проф. Д. Менделеева. I. Вступление
2. Вопросы этики и вопросы хозяйства в истории. Проф. Л. Брентано (пер. П. Берлина)
3. Изследование мировых пространств реактивными приборами. К. Циолковскаго
4. Немецкая литература в XIX столетии. Мейера (пер. А. Филипповой).
5. Сен-Симон и сен-симонизм. (Окончание). X. Инсарова
6. Невидимые лучи света. Проф. Д. А. Гольдгаммера
7. Литературные образы мнения: разсказы Куприна, Бунина, Серафимовича, Телешова и Юшкевича. Не страшное В. Короленки. „Чеховщина“; в текущей русской литературе. О правде и лжи, борьбе и раздумье. Е. Аничкова
8. Загадка Шекспира в трагедии „Гамлет“. Тень короля Гамлета. С. Москаленки
9. Философския письма: и. Творчество личности. М. Филиппова.
10. Трудовая теория ценности и ея критики. А. Финна
11. Научныя новости. (Под ред. проф. С. П. Глазенапа)
12. Обзор печати. В. Т — ца

ОТДЕЛ ВТОРОЙ.
13. Он и они. С. Бердяева
14. Барышня. (Драма). Стриндберга.
15. Cтиxoтвоpeниe H. З.
16. Хлеб насущный. Клары Фиттиг (пep. П. Гиберман). В приложении.

---

ОТДЕЛ ТРЕТИЙ.
17. Народный Университет. Лассар Кон. Химия обыденной жизни.

---

Изследование мировых пространств реактивными приборами

Небольшие аэростаты с автоматически наблюдающими приборами, без людей, до сих пор поднимались только до высоты, не большей 20 верст.

Трудность поднятия в высоту с помощию воздушных шаров возрастает чрезвычайно быстро с увеличением этой высоты.

Положим, мы хотим, чтобы аэростат поднялся на высоту 27 километров и поднял груз в 1 килограмм (2,4 фунта). Воздух на высоте 27 килом. имеет плотность около ¹/₅₀ плотности воздуха при обыкновенных условиях (760 мм. давления и 0° Цельсия). Значит шар на такой высоте должен занять объем в 50 раз больший, чем внизу. У уровня же океана следует впустить в него не менее 2 кубич. метров водорода, которые на высоте займут 100 куб. метров. При этом шар поднимет груз в 1 килограмм, т. е. поднимет автоматический прибор, а сам шар будет весить килограмм или около того.

Поверхность его оболочки, при диаметре в 5,8 метра, составит не менее 103 кв. метров. Следовательно каждый квадратный метр материи, считая и пришитую к ней сетку, должен весить 10 граммов, или квадр. аршин будет весить около 1-го золотника.

Кв. метр этой писчей бумаги весит 100 граммов; вес же кв. метра папиросной бумаги составляет граммов 50. Так что даже папиросная бумага будет в 5 раз тяжелее той материи, которая должна быть употреблена на наш аэростат. Такая материя, в применении к аэростату, невозможна, потому что оболочка, сделанная из нея, будет рваться и сильно пропускать газ.

Шары больших размеров могут иметь более толстую оболочку. Так шар с небывало большим диаметром в 58 метров будет иметь оболочку, каждый квадратный метр которой весит около 100 граммов, т. е. чуть тяжелее обыкновенной писчей бумаги. Подымет он 1000 килогр. груза, или 61 пуд, что черезчур много для самопишущаго прибора.

Если ограничиться, при тех же громадных размерах аэростата, подъемною силою в 1 килограмм, то оболочку можно сделать раза в 2 тяжелее. Вообще, в таком случае, аэростат хотя и обойдется весьма дорого, но построение его нельзя считать делом невозможным. Объем его на высоте 27 килом. составит 100.000 куб. метров, поверхность оболочки — 10.300 кв. метров.

А между тем какие жалкие результаты! Поднятие на какие-то 25 верст...

Что же сказать о поднятии приборов на большую высоту! Размеры аэростатов должны быть еще значительно больше, но не надо при этом забывать, что с увеличением размеров воздушнаго шара разрывающия оболочку силы все более и более берут поревес над сопротивлением материала.

Высота атмо- сферы в ки- лометрах.	Температура по Цельсию.	Плотность воздуха.
0 6 12 18 24 30 36 42 48 54,5	0 -30 -60 -90 -120 -150 -180 -210 -240 -272	1: 1:2 1:4,32 1:10,6 1:30,5 1:116 1:584 1:3900 1:28.000 0.

За пределы атмосферы поднятие приборов, с помощию воздушнаго шара, разумеется совсем немыслимо; из наблюдений над падающими звездами видно, что пределы эти не простираются далее 200 — 300 километров.

Теоретически даже определяют высоту атмосферы в 54 километра, принимая в основание расчета понижение температуры воздуха в 5° Цельсия на каждый километр поднятия, что довольно близко к действительности, по крайней мере для доступных слоев атмосферы.

Выше приведена таблица высот, температур и плотностей воздуха, вычисленная мною на этом основании. Из нея очевидно, как быстро возрастают трудности поднятия, с увеличением его высоты.

Делитель последняго столбца и выражает эту трудность устроения воздушнаго шара.

Перейдем к другой идее поднятия, — с помощию пушечных ядер.

На практике, начальная быстрота их движения не превышает 1200 метров в секунду. Такое ядро, пущенное вертикально, поднимется на высоту в 73 километра, если поднятие совершается в безвоздушном пространстве. В воздухе, разумеется, поднятие много меньше, в зависимости от формы и массы ядра.

При хорошей форме поднятие может достигать значительной величины, но помещать наблюдающие приборы внутри ядра невозможно потому что они будут разбиты в дребезги — или при возвращении ядра на землю, или при самом движении его в пушечном стволе..

Опасность при движении ядра в канале меньше, но и эта опасность, для целости аппаратов, громадна. Положим, для простоты что давление газов на ядро равномерно, вследствие чего, ускорение его движения в секунду составляет (W) метров. Тогда тоже ускоpeниe получают и все предметы в ядре, принужденные совершать с ним одно движенее. От этого внутри ядра должна развиться относительная, кажущаяся тяжесть, равная где (g) есть ускорение земной тяжести у поверхности земли.

Длина пушки (L) выразится формулой

, где

(V) есть скорость, приобретаемая ядром по выходе из жерла.

Из формулы видно, что (W), а следовательно и приращение относительной тяжести в ядре уменьшается с увеличением длины пушки, при постоянном (V); т. е. чем длиннее пушка, тем приборы безопаснее во время выталкивания ядра. Но и при очень длинной, неосуществимой на деле пушке, кажущаяся в ядре тяжесть, при ускоряющемся его движении в пушечном канале, настолько велика, что нежно устроенные аппараты едва ли могут перенести ее без порчи. Тем более невозможно послать в ядре что нибудь живое, если бы в этом случилась надобность.

Итак допустим, что построена пушка ну хоть в 300 метров высоты. Пусть она расположена вдоль башни Эйфеля, которая, как известно, имеет такую же высоту, и пусть ядро равномерным давлением газов получает, при выходе из жерла, скорость, достаточную для поднятия за пределы атмосферы, напр. для поднятия на 300 килом. от земной поверхности. Тогда потребную для этого скорость (V) вычислим по формуле V = , где (h) высота поднятия; — (получим около 2450 м. в 1 секунду). Из двух последних формул, исключая (V), найдем; <

/table> выражает относительную, или кажущуюся тяжесть в ядре. По формуле найдем, что оно ровно 1001.

Следовательно тяжесть всех приборов в ядре должна увеличиться в 1000 раз слишком, т. е. предмет весом в один фунт испытывает от кажущейся тяжести давление в 1000 фунтов или 25 пудов. Едва ли какой физический прибор выдержит подобное давленее.

Чтобы не ввести кого нибудь в заблуждение словом „относительная или кажущаяся тяжесть“, скажу, что я тут подразумеваю силу, зависящую от ускоряющагося движения тела (напр. ядра); она появляется также и при равномерном движении тела, если только это движение криволинейно, и называется тогда центробежной силой. Вообще она появляется всегда на теле или в теле, если только на одно это тело действует какая либо механическая сила, нарушающая движение тела по инерции.

Относительная тяжесть существует до тех пор, пока существует рождающая ее сила: прекращается последняя — исчезает безследно и относительная тяжесть. Если я называю эту силу тяжестью, то только потому, что ея временное действие совершенно тождественно с действием силы тяготения. Как тяготению подвержена каждая материальная точка тела, так и относительная тяжесть рождается в каждой частице тела, заключеннаго в ядре; происходит это потому, что кажущаяся тяжесть зависит от инерции, которой одинаково подвержены все материальныя части тела.

Итак, приборы внутри ядра сделаются тяжелее в 1001 раз. Если бы даже при этом страшном, хотя и кратковременном (0,24 секунды) усилении относительной тяжести и удалось их сохранить в целости, то все же найдется много других препятствий для употребления пушек в качестве посылателей в небесное пространство.

Прежде всего трудность их построения даже в будущем; далее — громадная начальная скорость ядра; действительно, в нижних густых слоях атмосферы, скорость ядра много потеряет вследствие сопротивления воздуха; потеря же скорости сильно сократит и величину поднятия ядра; затем трудно достигнуть равномернаго давления газов на ядро во время его движения в стволе, от чего усиление тяжести будет много более, чем мы вычислили (1001); наконец, безопасное возвращение ядра на землю более, чем сомнительно.

Реактивный прибор — „ракета“.

Впрочем, одного громаднаго усиления тяжести совершенно достаточно, чтобы оставить мысль о применении пушек к нашему делу.

Вместо их, или аэростата, в качестве изследователя атмосферы, предлагаю реактивный прибор, т.е. род ракеты, но ракеты грандиозной и особенным образом устроенной. Мысль не новая, но вычисления, относящияся к ней, дают столь замечательные результаты что умолчать о них было бы большим грехом.

Эта моя работа далеко не разсматривает всех сторон дела и совсем не решает его с практической стороны — относительно осуществимости; но в далеком будущем уже виднеются сквозь туман перспективы до такой степени обольстительныя и важныя, что о них едва ли теперь кто мечтает.

Представим себе такой снаряд: металлическая продолговатая камера (формы наименьшаго сопротивления), снабженная светом, кислородом, поглотителями углекислоты, миазмов и других животных выделений, — предназначена не только для хранения разных физических приборов, но и для управляющаго камерой разумнаго существа (будем разбирать вопрос по возможности шире). Камера имеет большой запас веществ, которыя при своем смешении тотчас же образуют взрывчатую массу. Вещества эти правильно и довольно равномерно взрываясь в определенном для того месте, текут в виде горячих газов по расширяющимся к концу трубам, вроде рупора или духового музыкальнаго инструмента. Трубы эти расположены вдоль стенок камеры, по направлению ея длины. В одном узком конце трубы совершается смешение взрывчатых веществ: тут получаются сгущенные и пламенные газы. В другом, расширенном ея конце они, сильно разредившись и охладившись от этого, вырываются наружу, через раструбы, с громадною относительною скоростью.

Понятно, что такой снаряд, как и ракета, при известных условиях, будет подниматься в высоту.

Необходимы автоматические приборы, управляющие движением ракеты (так будем мы иногда называть наш прибор) и силою взрывания по заранее намеченному плану.

Схематический вид ракеты.* Оба жидких газа разделены перегородкой. (А) есть место смешения газов и взрывания их. (В) — вылет сильно разреженных и охлажденных паров. Труба АВ окружена кожухом с быстро циркулирующей в нем металлической жидкостью.

*Рисунка в статье нет — Хл

Если равнодействующая сил взрывания не проходить точно через центр инерции снаряда, то снаряд будет вращаться и следовательно никуда не будет годится. Добиться же математической точности в этом совпадении совершенно невозможно, потому что как центр инерции не может не колебаться вследствие движения заключенных в снаряде веществ, так и направление в пушке равнодействующей, сил давления газов не может иметь математически-неизменное направление. В воздухе еще можно направлять снаряд рулем, подобным птичьему, но что вы сделаете в безвоздушном пространстве, где эфир едва-ли представит какую-либо заметную опору?

Дело в том, что если равнодействующая по возможности близка к центру инерции снаряда, то вращение его будет довольно медленно. Но едва только оно начинается, мы перемещаем какую-нибудь массу внутри снаряда до тех пор, пока происходящее от этого перемещение центра инерции не заставит снаряд уклоняться в противоположную сторону. Таким образом, сдедя за снарядом и перемещая внутри его небольшую массу, достигнем колебания снаряда то в ту, то в другую сторону, общее же направление действия взрывчатых веществ и движения снаряда изменяться не будет.

Может быть ручное управление движением снаряда окажется не только затруднительным, но и прямо практически невозможным. В таком случае следует прибегнуть к автоматическому управлению.

Основания для таковаго, после сказаннаго, понятны.

Притяжение земли не может быть тут основной силой для регулирования, потому что в ядре будет только относительная тяжесть с ускорением (W), направление которой совпадает с относительным направлением вылетающих взрывчатых веществ или прямо противоположно направлению равнодействующей их давления. А так как это направление меняется с поворачиванием ядра и пушки, то тяжесть эта, как направитель регулятора, не годится.

Возможно употребить для этой цели магнитную стрелку, или силу солнечных лучей, сосредоточенных с помощию двояко-выпуклаго стекла. Каждый раз, когда ядро с пушкой поворачивается, маленькое и яркое изображение солнца меняет свое относительное положениe в ядре, что может возбуждать расширение газа, давление, электрический ток и движение массы, возстановляющей определенное направление пушки, при котором светлое пятно падает в нейтральное, так сказать, нечувствительное место механизма.

Автоматически подвигаемых масс должно быть две.

Основною для регулятора направления ядра также может служить небольшая камера с двумя быстро вращающимися в разных плоскостях кругами. Камера привешена так, что положение или, точнее, направление ея не зависит от направления пушки. Когда пушка поворачивается, камера, в силу инерции, пренебрегая трением, сохраняет прежнее абсолютное направление (относительно звезд); это свойство проявляется в высшей степени при быстром вращении камерных дисков.

Прицепленныя к камере тонкия пружинки, при поворачивании пушки, меняют в ней свое относительное положение, что может служить причиною возникновения тока и передвижения регулирующих масс.

Наконец, поворачивание конца раструба также может служить средством сохранения определеннаго направления снаряда.

Преимущества ракеты.

Прежде чем излагать теорию ракеты или подобнаго ей реактивнаго прибора, попытаюсь заинтересовать читателя преимуществами ракеты перед пушкой с ея ядром.

а) Аппарат наш, сравнительно с гигантской пушкой, легок, как перышко; b) он относительно дешев и сравнительно легко осуществим; с) давление взрывчатых веществ, будучи довольно равномерным, вызывает равномерно-ускоряющееся движение ракеты, которое развивает относительную тяжесть; величиною этой временной тяжести мы можем управлять по желанию, т. е., регулируя силу взрыва, мы в состоянии сделать ее произвольно мало или много превышающей обыкновенную земную тяжесть. Если продположим, для простоты, что сила взрыва, понемногу уменьшаясь, пропорциональна массе снаряда, сложенной с массою оставшихся невзорванными взрывчатых веществ, — то ycкоpeниe снаряда, а следовательно и величина относительной тяжести будут постоянны. Итак, в ракете могут безопасно, в отношении кажущейся тяжести, отправиться не только измерительные приборы, но и люди; тогда как в пушечном ядре, даже при огромной, небывалой пушке, величиною с башню Эйфеля, относительная тяжесть увеличивается в 1001 раз. d). Еще не малое преимущество ракеты: скорость ея возрастает в желаемой прогрессии и в желаемом направлении; она может быть постоянной и может равномерно уменьшаться, что даст возможность безопаснаго спуска на планету. Все дело в хорошем регуляторе взрывания. е) При начале поднятия, пока атмосфера густа и сопротивление воздуха при большой скорости огромно, ракета двигается сравительно не быстро и потому мало теряет от сопротивления среды и мало нагревается.

Скорость ракеты, естественным образом, лишь медленно возрастает; но затем, по мере поднятия в высоту и разрежения атмосферы, она может искусственно возрастать быстрее; наконец, в безвоздушном пространстве, эта быстрота возрастания может быть еще усилена. Таким путем мы потратим „minimum” работы на преодоление сопротивления воздуха.

Ракета в среде, свободной от тяжести и атмосферы.

Сначала разсмотрим действие взрыва в среде, свободной от тяжести и окружающей материи, т. е. атмосферы. Относительно последней мы беремся только разобрать ея сопротивление движению снаряда, но не движению вырывающихся стремительно паров. Влияние атмосферы на взрыв не совсем ясно: с одной стороны оно благоприятно, потому что вырывающияся вещества имеют в окружающей материальной среде некоторую опору, которую они, при своем движении, увлекают и таким образом способствуют увеличению скорости ракеты; но с другой стороны, та же атмосфера, своей плотностью и упругостью мешает расширению газов далее известнаго предела, от чего взрывчатыя вещества не приобретают той скорости, которую они могли бы приобрести, взрываясь в пустоте. Это последнее влияние неблагоприятно, потому что приращение скорости ракеты пpoпopциoнально скорости отбрасываемых продуктов взрыва.

Массу снаряда со всем содержимым, кроме запаса взрывчатых веществ обозначим через M₁; полную массу последних через M₂; наконец, переменную массу взрывчатых веществ, оставшихся невзорванными в снаряде в данный момент — через М.

Таким образом, полная масса ракеты, при начале взрыва будет равна (M₁+M₂); спустя же некоторое время, она выразится переменною величиною M₁+M); наконец, пo окончании взрывания, — постоянной M₁

Чтобы ракета получила наибольшую скорость, необходимо чтобы отбрасывание продуктов взрыва совершалось в одном направлении относительно звезд. А для этого нужно, чтобы ракета не вращалась; а чтобы она не вращалась, надо чтобы равнодействующая взрывающих сил, проходящая через центр их давления, проходила в то же время и через центр инерции всей совокупности летящих масс.

Вопрос, как этого достигнуть на практике, мы уже слегка разобрали.

Итак, предполагая такое наивыгоднейшее отбрасывание газов в одном направлении, получим следующее дифференциальное уравнeниe, на основании закона о постоянстве количества движения:

1...dVM₁+M)=V₁.dM.

Здесь dM есть безконечно-малый отбросок взрывчатаго вещества, вырывающагося из пушечнаго раструба с постоянною относительно ракеты скоростью (V₁)

Я хочу сказать, что относительная скорость (V₁) вырывающихся элементов, при одинаковых условиях взрыва, одна и та же во все время взрывания, — на основании закона относительных движений; (dv) есть приращение скорости (V) движения ракеты вместе с оставшимися нетронутыми взрывчатыми материалами; приращение это (dV) совершается, благодаря отбрасыванию элемента (dM) со скоростию (V₁). Определением последней мы займемся в своем месте.

Разделяя переменныя величины в уравнении 1 и интегрируя, получим:

Тут С есть постоянное. Когда М=M₂, т. е. до взрывания, V=0; на этом основании найдем:

4... C= — Lnat M₁+M₂); *)

)* (Lnat) есть натуральный логарифм
стало быть

Знаки обеих частей уравнения обратные, потому что скорости V и V₁ противоположны по направлению.

Наибольшая скорость снаряда получится, когда М=0, т. е. когда весь запас (M₂) взорван; тогда получим, полагая в предыдущем уравнении M=0:

Отсюда мы видим, что скорость (V) снаряда возрастает неограниченно с возрастанием количества (M₂) взрывчатых веществ. Значить, запасаясь разными количествами их, при разных путешествиях, мы получим самыя разнообразныя окончательныя скорости. Из уравнения 6 также видно, что скорость ракеты, по израсходовании определеннаго запаса взрывчатаго вещества, не зависит от быстроты или неравномерности взрывания, лишь бы частицы отбрасываемаго материала двигались с одной и тою же скоростью (V1) относительно ядра.

Однако, с увеличением запаса (M₂), скорость (V) ракеты возрастает все медленнее и медленнее, хотя и безгранично. Приблизительно, она возрастает, как логарифм от увеличения количества взрывчатых запасов (M₂), (если M₂ велико в сравнении с М1 т. е. масса взрывчатых веществ в несколько раз больше массы снаряда).

Дальнейшия вычисления будут интересны, когда мы определим (V₁), т. е. относительную и окончательную скорость взорваннаго элемента.

Так как газ или пар, при оставлении пушечнаго раструба, весьма разрежается и охлаждается (при достаточной длине трубы) — даже обращается в твердое состояние, в пыль, которая мчится с страшною быстротою, — то можно принять, что вся энергия горения, или химическаго соединения, при взрывании, обращается в движение продуктов горения, или в кинетическую энергию. В самом деле, представим себе определенное количество газа, расширяющагося в пустоте, без всяких приборов: он будет во все стороны расширяться и вследствие этого охлаждаться до тех пор, пока не превратится в капли жидкости, или в туман.

Туман этот обращается в кристаллики, но уже не от расширения, а от испарения и лучеиспускания в мировое пространство.

Расширяясь, газ выделит всю свою явную и отчасти скрытую энергию, которая превратится в конце концев в быстрое движение кристалликов, направленное во все стороны, так как газ расширялся свободно во все стороны.

Если же его заставить расширяться в резервуаре с трубой, то труба направит движение газовых молекул по определенному направлению, чем мы и пользуемся для наших целей, т. е. для движения ракеты.

Как будто энергия движения молекул превращается в кинетическое движение до тех пор, пока вещество сохраняет газообразное или парообразное состояние. Но это не совсем так. Действительно, часть вещества может обратиться в жидкое состояние; но при этом выделяется энергия (скрытая теплота парообразования), которая передается оставшейся парообразной части материи и замедлит на некоторое время переход ея в жидкое состояние. Подобное явление мы видим в паровом цилиндре, когда пар работает собственным расширением, выход же из парового котла в цилиндр заперт. Тогда, при какой бы температуре не был пар, часть eгo обращается в туман, т.е. жидкое состояние, другая же часть продолжает сохранять парообразное состояние и работать, заимствуя скрытую теплоту сгустившихся в жидкость паров.

Итак, энергия молекулярная будет превращаться в кинетическую, по крайней мере, до состояния жидкаго. Когда вся масса обратится в капли, превращение в кинетическую энергию почти приостановится, потому что пары жидких и твердых тел, при низкой температуре, имеют черезчур незначительную упругость и использование их на практике затруднительно, так как потребует огромных труб.

Однако некоторая незначительная часть указанной нами энергии пропадет для нас, т. е. не превратится в кинетическую энергию, благодаря трению о трубу и лучеиспусканию теплоты нагретыми ея частями. Впрочем, труба из красной меди может быть окружена кожухом, в котором циркулирует какой нибудь жидкий металл; он передаст жар весьма нагретой части одного конца трубы другой ея части, охлажденной вследствие сильного разрежения паров. Таким образом и эта потеря, от лучеиспускания и теплопроводности, может быть утилизирована или сделана очень незначительной. В виду кратковременности взрывания, продолжающагося в крайних случаях от 2 до 5 минут, потеря от лучеиспускания и без всяких приспособлений незначительна; циркуляция же металлической жидкости в кожухе, окружающем трубы, необходима для другой цели: для поддержания труб при одной и той же невысокой температуре, т. е. для сохранения крепости трубы. Несмотря на это, возможно, что часть ея будет расплавлена, окислена и унесена вместе с газами и парами. Может быть, для избежания этого, внутреннюю часть трубы будут выкладывать каким-нибудь особенным огнеупорным материалом, углеродом, известью (СаО.) или чем-нибудь иным. Хотя часть углерода при этом и сгорит, но крепость металлической пушки, мало нагретой, пострадать от этого не может.

Газообразный же продукт горения углерода — углекислота только усилит поднятие ракеты. Может быть употреблен будет род тигельнаго материала — какая-нибудь смесь веществ. Во всяком случае, не я решу этот вопрос, как и множество других, относящихся к нашим реактивным приборам.

Во многих случаях я принужден лишь гадать или предполагать. Я нисколько не обманываюсь и отлично знаю, что не только не решаю вопроса во всей полноте, но что остается поработать над ним в 100 раз больше, чем я поработал. Моя цель возбудить к нему интерес, указав на великое значение его в будущем и на возможность его решения...

Для уменьшения протяжения, занимаемаго трубами, при той же длине их, можно завивать их кольцами или змеевиком, окруженным, для сохранения умеренной и равномерной температуры, хорошо проводящей тепло и быстро циркулирующей жидкостью.

В настоящее время обращение водорода и кислорода в жидкость не представляет особенных затруднений. Жидкости эти должны быть разделены перегородкой. Температура их весьма низкая; поэтому ими полезно окружать или кожухи с циркулирующим металлом, или непосредственно самыя пушки.

Опыт покажет как сделать лучше. Но в последнем случае для труб медь уже не годится, потому что она при очень низкой температуре делается хрупкой и, вероятно, теряет свою вязкость. Некоторые же металлы, напротив, делаются крепче от охлаждения; вот такие то металлы и нужно тогда употребить, напр., железо. Не помню хорошо, но какие то опыты, над сопротивлением, кажется, железа, в жидком воздухе, указали, что вязкость его при этой низкой температуре увеличивается чуть ли не в десятки раз. За достоверность не ручаюсь, но опыты эти в применении к нашему делу, заслуживают глубочайшаго внимания. (Почему бы не охлаждать таким образом и обыкновенныя пушки, прежде чем из них стрелять; ведь жидкий воздух теперь такая обыкновенная вещь).

Жидкий кислород и такой же водород, выкачиваемые из своих резервуаров, в известном отношении, в узкое начало трубы и соединяясь тут понемногу, могут дать прекрасный взрывчатый материал. Получаемый при химическом соединении этих жидкостей водяной пар, при страшно высокой температуре, будет расширяться, подвигаясь к концу, или устью трубы до тех пор, пока не охладится до того, что обратится в жидкость, несущуюся в виде тончайшаго тумана по направлению длины трубы, к ея выходу (раструбу).

Водород и кислород в жидком виде, прежде чем попасть в пушку, пройдут по особому кожуху, вдоль ея поверхности, охладят ее, сами нагреются и тогда уже попадают в пушку и взрываются; таким образом, энергия тепла, уходящаго путем теплопроводности и лучеспускания из пушки опять в нее возвращается, чтобы обратиться в энергию поступательнаго движения пара или тумана.

Водород и кислород, в газообразном состоянии, соединяясь для образования одного килограмма воды, развивают 3825 калорий. Под словом „калория" мы тут подразумеваем количество теплоты, потребное для нагревания на 1° Цельсия одного килограмма воды.

Количество это (3825) у нас будет немного меньше, раз кислород и водород находятся в жидком состоянии, а не в газообразном, к каковому относится данное нами число калорий. В самом деле, жидкости, во-первых, надо нагреть, во-вторых обратить в газообразное состояние, на что расходуется некоторая энергия. В виду незначительной величины этой энергии, сравнительно с энергией химической, мы оставим наше число без умаления.

Принимая механический эквивалент теплоты в 424 килограмметра, найдем, что 3825 калорий соответствуют работе в 1.621. 800 килограмметров; этого достаточно дли поднятия продуктов взрыва, т. е. одного килограмма вещества, на высоту 1.622 киллометра от поверхности земного шара, предполагая силу тяжести постоянной. Эта работа, превращенная в движение, соответствует работе одного килограмма массы, движущейся со скоростью 5.700 метров в 1 секунду. Я не знаю ни одной группы тел, которыя, при своем химическом соединении, выделяли бы, на единицу массы полученнаго продукта, такое огромное количество энергии. Kpoме того, некоторыя другия вещества, соединяясь, не образуют летучих продуктов, что для нас совсем не годится.

Так кремний, сгорая в кислороде (Si+O2= Si O2), выделяет огромное количество тепла, именно 3654 калории на единицу массы полученнаго продукта (Si O2), но к сожалению образуются трудно-летучия тела.

Приняв жидкий кислород и водород за материал, наиболее пригодный для взрывания, я дал число для выражения их взаимной химической энергии, приходящейся на единицу массы полученнаго продукта (Н2 О), несколько большее истиннаго, так как вещества, соединяющияся в ракете, должны находиться в жидком, а не в газообразном состоянии, и кроме того при очень низкой температуре.

Считаю не лишним тут утешить читателя, что не только на эту энергию (3825 кал.), но и на несравненно большую мы можем надеяться в будущем, когда может быть найдут возможным осуществить наши недовольно разработанныя еще мысли. В самом деле, разсматривая количество энергии, получаемыя от химических процессов разнообразных веществ, замечаем в общем, не без исключений конечно, что количество энергии, приходящейся на единицу массы продуктов соединения, зависит от атомных весов (в большинстве случаев) соединяющихся простых тел: чем меньше атомные веса тел, тем более выделяется при соединении их тепла. Так, при образовании сернистаго газа (SО2), образуется только 1250 калорий, а при образовании окиси меди (СиО) — только 546 калорий; между тем как уголь, при образовании углекислоты (СО2), выделяет на единицу ея массы 2204 калории. Водород с кисдородом, как мы видели, выделяют еще больше (3825). Для оценки этих данных, к применению в высказанной мною идеи, напомню тут величину атомных весов приводимых элементов: водород = 1; кислород = 16; углород = 12; сера = 32; кремний = 28; медь = 63.

Конечно, можно привести и много исключений из этого правила, но в общем оно справедливо. Действительно, если мы вообразим ряд точек, абсциссы которых выражают сумму (или произведение) атомных весов соединяющихся простых тел, а ординаты соответствующую энергию химическаго соединения, то, проведя через точки (по возможности ближе к ним) плавную кривую, увидим непрерывное уменьшение ординат по мере увеличения абсцисс, чем и доказывается наш взгляд.

Поэтому, если когда-нибудь так называемыя простыя тела окажутся сложными и их разложат на новые элементы, то атомные веса последних должны быть меньше известных нам простых тел. Новооткрытые элементы, по предыдущему, при своем соединении, должны выделять при своем соединении несравненно большое количество энергии, чем тела, считаемыя теперь условно простыми и имеющия сравнительно большой атомный вес.

Об ионах, или подъатомах давно уже высказывались и даже думают, что условные элементы разлагаются на эти иoны под влиянием солнечнаго света.

Самое существование эфира с его почти бозпредельною упругостью и громадною скоростью его атомов, указывает на безпредельно малый атомный вес этих атомов и безпредельную энергию в случае их химическаго соединения.

Как бы то ни было, но пока для V₁ (см. 15 и 16) мы не можем принять более 5700 метров в 1 секунду. Но со временем кто знает, может быть это число увеличится в несколько раз.

Принимая 5700 метров, можем по формуле 16 вычислить не только отношение скоростей , но и абсолютную величину окончательной (наибольшей) скорости (V) снаряда в зависимости от отношения

Из формулы 6 видно, что масса ракеты со всеми пассажирами и всеми аппаратами (М1) может быть произвольно велика и скорость (V) снаряда от этого нисколько не потеряет, лишь бы запас взрывчатых веществ (M₂) возрастал пропорционально возрастанию массы (М1) ракеты. Итак, всевозможной величины снаряды, с любым числом путешественников, могут приобретать скорости желаемой величины. Впрочем возрастание скорости ракеты сопровождается, как мы видели, несравненно быстрейшим возрастанием массы (M₂) взрывчатых воществ. Поэтому насколько легко и возможно увеличение массы поднимающагося в небесное пространство снаряда, настолько затруднительно увеличение его скорости.

Из уравнения 6 получим следующую таблицу:

, тут

		Секундная скорость (V) в метрах			Секундная скорость (V) в метрах
0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6	0,095 0,182 0,262 0,336 0,405 0,693 1,098 1,386 1,609 1,792 1,946	543 1.037 1.493 1.915 2.308 3.920 6.260 7.880 9.170 10.100 11.100	7 8 9 10 19 20 30 50 100 193 Безконечно.	2,079 2,197 2,303 2,398 2,996 3,044 3,434 3,932 4,615 5,268	11.800 12.500 13.100 13.650 17.100 17.330 19.560 22.400 26.280 30.038 Безконечно.

Из нея усматриваем, что скорости, получаемыя реактивным путем далеко не малы. Так при массе взрывчатых веществ, в 193 раза превышающей вес M₁) снаряда (ракеты), скорость его, по окончании взрывания и израсходования всего запаса (M₂), равна скорости движения земли вокруг солнца. Не думайте, что такая громадная масса взрывчатаго материала требует для своего сохранения громаднаго количества крепкаго материала для сосудов, содержащих взрывчатые элементы. Действительно, водород и кислород в жидком виде только тогда обнаруживают высокое давление, когда сосуды, содержащие их, заперты, т. е. когда самые газы, влиянием окружающих сравнительно теплых тел, нагреваются. У нас же эти ожиженные газы должны иметь свободный выход в трубу (помимо постояннаго притока их туда в жидком виде), где они, соединяясь химически, взрывают. Непрерывное и быстрое течение газов, соответствующее испарению жидкостей, охлаждает эти последния до того, что оне, своими парами, не производят почти никакого давления на окружающия их стенки. Итак, для сохранения элементов взрыва, не требуется на сосуд большой массы вещества.

Когда запас взрывчатаго вещества равен массе ракеты , то скорость последней чуть не вдвое более той, которая нужна, чтобы камню или пушечному ядру, пущенному „селенитами" с поверхности нашей луны, удалиться от нея навсегда и сделаться спутником земли, второй луной.

Эта скорость (3920 метров в секунду) почти достаточна для вечнаго удаления тел, брошенных с поверхности Марса или Меркурия.

Если отношение масс будет 3, то уже получится, по израсходовании всего запаса, такая скорость снаряда, которой лишь немного не достает для того, чтобы он мог вращаться, за пределами атмосферы, вокруг земли, подобно ея спутнику.

При отношении , равном 6, скорость ракеты почти достаточна для удаления ея от земли и вечнаго вращения вокруг солнца в качеств самостоятельной планеты. При большем количестве взрывчатаго запаса, возможно достижение пояса Астероидов и даже тяжелых планет.

Из таблицы видно, что и при небольшом запасе взрывчатых веществ, окончательная скорость снаряда еще достаточна для практических целей. Так при запасе, составляющем лишь 0,1 веса ракеты, скорость равна 543 метрам в секунду, что довольно для поднятия ракеты на 15 километров. Далее, из таблицы мы видим, что при незначительном запасе, скорость, по окончании взрыва, приблизительно, пропорциональна мaccе запаса (M₂); следовательно, в этом случае, высота поднятия пропорциональна квадрату этой массы (M₂) запаса. Так, при заnacе составляющем половину массы ракеты , последняя залетит далеко за пределы атмосферы.

Интересно определить, какая часть полной работы взрывчатых веществ, т. е. их химической энергии, передается ракете

Работа взрывчатых веществ выразится , где (g) есть ycкоpeниe земной тяжести; механическая работа ракеты, имеющей скорость (V) выразится в тех же единицах: или на основании формулы 6:

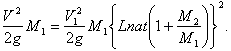
Разделив теперь работу ракеты на работу взрывчатаго матеpиaлa, получим:

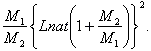
По этой формуле вычислим следующую таблицу утилизации ракетой энергии взрывчатых веществ.

Из формулы и таблицы видно, что при очень малых количествах взрывчатаго материала утилизация его равна отношению , т. е. тем меньше, чем относительное количество взрывчатых веществ меньше.

	Утили- зация		Утили- зация
0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6	0,090 0,165 0,223 0,282 0,328 0,480 0,600 0,64 0,65 0,64 0,63	7 8 9 10 19 20 30 50 100 193 Безконечно	0,62 0,60 0,59 0,58 0,47 0,46 0,39 0,31 0,21 0,144 Нуль

Далее, с увеличением относительнаго количества взрывчатых веществ, утилизация возрастает и, приблизительно при учетверенном их количестве (сравнительно с массой ракеты) достигает наибольшей величины (0,65). Дальнейшее увеличение взрывчатых веществ, хотя и медленно, но непрерывно уменьшает их полезность; при безконечно-большом их количестве, она нуль, также как и при безконечно-малом. Из таблицы также видим, что при изменении отношения от 2 до 10, утилизация более половины; это значит, что в таком случае более половины потенциальной энергии взрывчатаго материала передается в виде кинетической энергии ракете.

---

Ракета под влиянием тяжести. Вертикальное поднятие.

Мы определили скорость, приобретаемую ракетой в пустоте и при отсутствии силы тяготения, в зависимости от массы ракеты, массы взрывчатых веществ и энергии их химическаго соединения.

Разберем теперь влияние постоянной силы тяжести на вертикальное движение снаряда.

Мы видели, что без влияния тяжести приобретаются ракетой огромныя скорости и утилизируется значительное количество энергии взрыва. Это будет справедливо и для среды тяжести, если только взрыв будет мгновенный. Но такой взрыв для нас не годится, потому что при этом получится убийственный толчек, котораго не вынесет ни снаряд, ни вещи и люди, заключенные в нем. Нам, очевидно, нужно медленное взрывание; при медленном же взрывании полезный эффект уменьшается и даже может обратиться в нуль.

Действительно, пусть взрывание будет настолько слабо, что ycкоpeниe ракеты, происходящее от него, будет равно ускорению (g) земли. Тогда снаряд, во все время взрывания, будет стоять в воздухе неподвижно, без опоры.

Конечно он не приобретет при этом никакой скорости и утилизация взрывчатых веществ, не смотря на их количество, будет равняться нулю. Итак, крайне важно изследовать аналитически влияние на снаряд тяготения.

Когда ракета двигается в среде, свободной от силы тяжести, то время (t), в течение котораго взрывается весь запас взрывчатаго вещества, равно:

7..., где (V) есть скорость снаряда по окончании взрыва, а (р) постоянное ускорение, сообщаемое ракете взрывчатыми материалами в 1 секунду времени.

Сила взрывания, т.е. количество веществ, расходуемых при взрыве в единицу времени, в этом простейшем случае равномерно ускоряющагося движения снаряда, — не постоянна, но не прерывно ослабляется — пропорционально уменьшению массы снаряда с остатком невзорванных материалов.

29. Зная (р), или ускорение в среде без тяжести, можем выразить и величину кажущейся (временной) тяжести внутри ракеты в течение ея ускоряющагося движения, или в течение времени взрывания.

Приняв силу тяжести у поверхности земли за единицу, найдем величину временной тяжести в снаряде равной , где (g) есть земное ускорение; формула эта показывает, во сколько раз давление на подставки всех вещей, помещенных в ракете, больше давления теx жe вещей, лежащих на столе в нашей комнате при обыкновенных условиях. Весьма важно знать величину относительной тяжести в снаряде, потому что она обусловливает целость или излом аппаратов и здоровье людей пустившихся в путь для изучения неизвестных пространств и свойственных им явлений.

При влиянии постоянной или переменной тяжести, любой силы, время в течение котораго расходуется один и тот же запас взрывчатaro материала, будет то-же, как и без влияния тягoтения; оно выразится известною нам формулою (см. 7) или следующею:

, где

(V₂) есть скорость ракеты по окончании взрывания в среде тяжести с постоянным ускорением (g); Тут, конечно, предполагается, что, (p) и (g) параллельны и противоположны (см. заглавие главы); (р — g) выражает видимое ускорение снаряда (относительно земли), являющееся результатом двух противоположных сил: силы взрыва и силы тяжести.

32. Действие последней на снаряд нисколько не влияет на относительную в нем тяжесть и она выражается без всякаго изменения формулой 9.... Напр., если р=0, т.е. если взрывания нет, то нет и временной тяжести, потому что =0. Это значит, что если взрывание прекратится и снаряд двигается в ту или другую сторону только под влиянием своей скорости и силы тяготения солнца, земли и других звезд и планет, то находящийся в снаряде наблюдатель ни сам не будет иметь, повидимому, ни малейшаго веса, — ни обнаружит его, при помощи самых чувствительных пружинных весов, ни в одной из вещей, находящихся при нем или в ракете. Падая или поднимаясь в ней под влиянием инерции даже у самой поверхности земли, наблюдатель не будет испытывать ни малейшей тяжести, пока, разумеется, снаряд не встречает никаких препятствий, — в виде, напр., сопротивления атмосферы, воды или твердаго грунта.

Если p=g, т. е. если давление взрывающихся газов равно тяжести снаряда (= 1), то относительная тяжесть будет равняться земной. Пpи начальной неподвижности, снаряд в этом случае и остается неподвижным во все время действия взрыва; если же до него снаряд имел какую нибудь скорость (вверх, в бок, в низ), то эта скорость так и останется без всякаго изменения, пока не израсходуется весь взрывчатый материал: тут тело, т. е. ракета уравновешена и двигается как бы по инерции в среде, свободной от тяжести.

На основании формул 8 и получим:

Отсюда, зная какую скорость (V2) должен иметь по окончании взрыва снаряд, мы вычислим (V), по которой, с помощию формулы 6, определим и потребное количество (М2) взрывчатых веществ.

Из уравнений 6 и 10 получим:

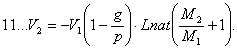
Из этой формулы, также как из предыдущей следует, что скорость, приобретаемая ракетой, меньше при влиянии тяготения, чем без него (6). Она (V2) может быть даже равна нулю не смотря на обилие взрывчатаго запаса, если=1, т.е. если ускоpeниe, сообщаемое снаряду взрывчатым материалом, равно ускорению земной тяжести, или — давление газов равно и прямо противоположно действию тяготения. (См. форм. 10 и 11).

В этом случае ракета стоит несколько минут неподвижно, нисколько не поднимаясь; когда же запас истощен, она падает, как камень.

Чем больше (р) по отношению к (g), тем большую скорость (V2) приобретает снаряд при данном количестве (M2) взрывчатых веществ (форм. 11).

Поэтому, желая подняться выше, надо сделать (р) как можно больше, т. е, производить взрыв как можно деятельнее. Однако, при этом, во-первых, требуется более крепкий и массивный снаряд, во-вторых, — более крепкие предметы и аппарады в снаряде, потому что (по 32) относительная тяжесть в нем будет весьма велика и в особенности опасна для живого наблюдателя, если таковый отправляется в ракете.

Во всяком случае, на основании формулы 11-ой, в пределе,

т. е., если (р) безконечно велико, или взрыв моментален, то скорость, (V2) ракеты в среде тяжести та-же что и в среде без тяжести.

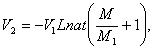
Согласно формуле 8 время взрывания не зависит от силы тяготения, а лишь исключительно от количества взрывчатаго матepиaлa и быстроты их взрывания (р).

39. Любопытно определить эту величину. Положим в форм. 7  V=11.100 метров (см. таблицу), a p=g=9,8 метра; тогда t = 1.133 секунды.

Значит в среде, свободной от тяжести, ракета пролетела равномерно ускоряющимся движением менее 19 минут — и это при ушестеренном количестве взрывчатых веществ сравнительно с массою снаряда (см. табл.).

При взрывании-же у поверхности нaшeй планеты, он простоял бы неподвижно в течении техъ-же 19 минут.

40. Если =1, то, по табл. V=3.920 метров; следовательно, t=400 секундам, или 6²/₃ минуты.

При = 0,1, V=543 метра, a t = 55,4 секунды, т. е. менее минуты. В последнем случае, у поверхности земли, снаряд простоял бы неподвижно 55½ секунд.

Отсюда мы видим, что взрывание у поверхности планеты, или вообще в среде, несвободной от силы тяжести, может быть совершенно безрезультатным, если происходит, хотя и долгое время, но с недостаточною силою: действительно, сиаряд остается на месте и не получает никакой поступательной скорости, если не приобрел ее раньше; в противном случае, он может совершить некоторое перемещение с равномерною скоростью. Если это перемещение совершается в верх, то снаряд сделает некоторую работу. В случае первоначальной горизонтальной скорости и перемещение будет горизонтально; работы тут не будет, но тогда снаряд может служить для такихъ-же целей, как локомотив, пароход, или управляемый аэростат. Служить для этих целей перемещения снаряд может только в течение нескольких минут, пока совершается взрывание, но и в такое небольшое время он может пройти значительное пространство.

Время стояния прибора в среде тяготения обратно пропорционально (g), т. е. силе этого тяготения.

Так на луне прибор простоял бы неподвижно без опоры (при = 6) в течение 2 часов.

А. Положим в формуле 8, для среды с тяжестью: =10; =6; тогда вычислим V2 = — 9990 метров. Относительная тяжесть, по предыдущаго будет равна 10, т. е. человек в 70 килограммов веcoм, во все время взрывания (около 2 минут) будет испытывать тяжесть в 10 раз большую, чем на земле и будет весить на пружинных весах 700 килограммов (пудов 40). Такую тяжесть путешественник может перенести без вреда только при соблюдении особых предосторожностей: при погружении в особую жидкость при особенных условиях.

На основании формулы на стр. 60, вычислим и время взрывания, или время этой усиленной тяжести; получим 113 секунд, т.е. менее двух минуть. Это очень немного и кажется с перваго раза поразительным, как может снаряд в течение такого ничтожнаго промежутка времени приобрести скорость, чуть недостаточную для удаления от земли и движения вокруг солнца подобно новой планете.

Мы нашли V2= — 9990 метров, т. е. такую скорость, которая лишь немного менее скорости (V), приобретаемой в среде свободной от силы тяготения, при тех же условиях взрыва (см. табл. I). Но так как снаряд во время взрывания еще и поднимается на некоторую высоту, то приходит даже в голову, что общая работа взрывчатых веществ совсем не уменьшилась сравнительно с работою их в среде без тяжести. Вопрос этот мы сейчас разберем.

Уcкopение снаряда в среде тяжести выразится р1 = р — g.

На разстоянии от поверхности земли, не превышающем нескольких сотен версть, мы (g) примем постоянным, что не повлечет за собой большой погрешности; да и погрешность то будет в неблагоприятную сторону, т. е. истинныя числа будут благоприятнее для полета, чем вычисленныя нами.

Высота (h) поднятия снаряда, во время (t) действия взрыва, будет.

выключая отсюда (t), по уравнению 31, получим: , где (V2) есть скорость снаряда в среде тяжести, по истощении всего взрывчатаго запаса.

Теперь получим, выключая (V2):

где (V) есть скорость, приобретаемая ракетой в среде, свободной от тяготения. Полезная работа взрывчатых веществ в такой среде выразится: Работа же (T1) в среде тяжести выразится в зависимости от высоты поднятия снаряда и его скорости по окончании взрыва; именно: Отношение этой работы к предыдущей, идеальной, равно: Исключив отсюда (h) и (V) найдем: т. е. работа в среде тяготения, получаемая от определеннаго количества взрывчатых веществ (М2), менее, чем в среде свободной от него; разница эта тем меньше, чем быстрее взрываются газы, или чем более (р). Напр., в случае А (стр. 65), потеря составляет только 1/10, а утилизация (18) равна 0,9. Когда p=g, или когда снаряд стоит в воздухе, не имея даже постоянной скорости, потеря будет полная (1), а утилизация равна нулю. Такова же будет утилизация, если снаряд имеет постоянную горизонтальную скорость.

В парагр. А мы вычислили V₂=9990 мотров. Применим формулу 13 к случаю А найдем: h=565 километров; значит, в течении взрыва, снаряд зайдет далеко за пределы атмосферы и приобретет еще поступательную cкopость в 9990 метров.

Заметим, что скорость эта на 1.110 метров меньше, чем в среде, свободной от силы тяготения. Эта разность составляет как раз 1/10 скорости в среде без тяжести (см. табл. 22).

Отсюда видно, что потеря в скорости подчиняется тому же закону, как и потеря работы (см. 51), что, впрочем, строго следует и из формулы 34, преобразуя которую, получим:

Найдем:

где (Т1) есть работа, получаемая снарядом от взрывчатых веществ в среде тяготения, сила которого равна (g).

Чтобы снаряд мог совершить все необходимые работы, поднимаясь в высоту, преодолевая сопротивление атмосферы и приобретая желаемую скорость, — необходимо, чтобы сумма всех этих работ равнялась (T1).

Определив все эти работы, с помощию формулы 56, вычислим Т. Зная же (Т), вычислим и (V), т. е. скорость в среде без тяжести, по формуле:

Зная теперь (V), можем разсчитать и потребную массу (M₂) взрывчатых веществ по формуле 16.

Таким путем, с помощию предыдущаго, найдем:

20... M₂=M₁ Вычисляя, мы заменили для краткости через (Т2).

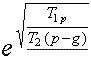
Итак, зная массу снаряда M₁) со всем содержимым кроме взрывчатаго материала (M₂), механическую работу (Т2) взрывчатых веществ при массе их, равной массе снаряда M₁) работу (Т), которую должен совершить снаряд при своем вертикальном поднятии, силу взрывания (р) и силу тяготения (g), — можем узнать и количество взрывчатых веществ (M₂), необходимое для поднятия массы M₁) снаряда.

Отношение в формуле не изменится, если его сократить на M₁). Так что под (T1) и (Т2) можно подразумевать механическую работу (T1), совершаемую единицею массы снаряда и механическую работу (Т2) единицы взрывчатых веществ.

Под (g) нужно, вообще, подразумевать постоянное сопротивление, равное сумме сил тяжести и сопротивления среды. Но сила тяготения постепенно убывает с удалением от центра земли, вследствие чего утилизируется большее количество механической работы взрывчатых веществ. С другой стороны, сопротивление атмосферы, будучи, как увидим, сравнительно с тяжестью снаряда, весьма незначительным, — уменьшает утилизацию энергии взрывчатых веществ.

По некотором размышлении увидим, что последняя убыль, продолжаясь недолгое время пролета через воздух, с избытком вознаграждается прибылью от уменьшения притяжения на разстояниях значительных (500 килом.), где кончается действие взрывчатых веществ.

Итак, формулу 20 можем смело применять к вертикальному поднятию снаряда, несмотря на осложнение от изменения тяжести и сопротивления атмосферы (g=9,8 метров).

---

Среда тяжести. Отвесное возвращение на землю.

Разсмотрим сначала остановку в среде, свободной от тяжести или моментальную остановку в среде тяжести. Пусть, напр., ракета силою взрыва некоторого (не всего) количества газов приобрела скорость 10.000 метров в секунду (см. табл. 22). Теперь, для остановки, следует приобрести такую же скорость, но в обратном направлении. Очевидно, количество оставшихся взрывчатых веществ, согласно таблице I, должно быть в 5 раз больше массы M₁) снаряда. Стало-быть снаряд должен иметь, по окончании первой части взрыва (для приобретения поступательной скорости), запас взрывчатаго вещества, масса котораго выразится через 5 M₁ = M₂.

Вся масса, вместе с запасом, составит M₂ + М1 = 5 М1 + М1 = 6 M₁.

Этой массе (6M₁) первоначальное взpываниe должно также сообщить скорость в 10.000 метров, а для этого нужно новое количество взрывчатаго материала, которое должно также в 5 раз (см. 22) превышать массу снаряда с массою запаса для остановки; т. е. мы должны ее (6M₁) увеличить в 5 раз; получим 30M₁, что вместе с запасом для остановки (5M₁) составит 35M₁.

Означив число табл. I, показывающее во сколько раз масса взрывчатаго материала больше массы снаряда, через (q) , предыдущия рассуждения, определяющия массу всего взрывчатаго вещества для приобретения скорости и уничтожения ея, выразим так:

21. =q+(1+q)· q = q (2+q), или прибавляя и вычитая единицу из второй части уравнения, получим: 22. = 1+2 q+q² = (1 — q)² — 1.

Всего же, с массою ракеты M₁, или 1) найдем: + 1 = (1 + q) ². Последнее выражение легко запомнить.

Когда (q) очень мало, то, приблизительно, количество взрывчатаго вещества равно 2 q (потому что (q² будет ничтожно), т. е. оно только вдвое больше; чем для одного приобретения скорости.

На основании полученных формул таблицы I, составим следующую таблицу:

Табл. II. В среде без тяжести.

V. Метры.	M2:M1.	M3:M1	V. Метры.	M2:M1.	M3:M1
543 1.037 1.493 1.915 2.308 3.920 6.260 7.880 9.170 10.100 11.100	0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6	0,21 0,44 0,69 0,96 2,25 3 8 15 24 35 48	11.800 12.500 13.100 13.650 17.100 17.330 19.560 22.400 26.280 30.038 Безконечно.	7 8 9 10 19 20 30 50 100 193	63 80 99 120 399 440 960 2.600 10.200 37.248 Безконечно.

Из нея видим, как неодолимо громаден запас взрывчатаго материала, если мы хотим приобрести очень большую скорорость и потерять ее.

Эту таблицу можем составить и посредством формулы 6, из которой имеем:

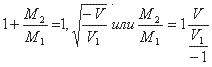
Заметим, что отношение, положительно, потому что скорости снаряда и газов противоположны по направлению и следовательно имеют разные знаки.

Полагая в последней формуле (V) вдвое большим, чем в первом столбце таблицы, получим отношение т. е. относительное количество взрывчатаго материала, потребное для приобретения скоростей последней таблицы и последующаго уничтожения их.

Если мы находимся в среде тяжести, то в простейшем случае вертикальнаго движения процесс остановки и опускания на землю будет такой: когда ракета, под влиянием приобретенной скорости поднялась на известную высоту и остановилась, то начинается ея падение на землю. Когда снаряд достигнет той точки, в которой окончилось при поднятии действие взрывчатых веществ, он снова подвергается влиянию остатка их, — в том же направлении и в том же порядке. Очевидно, к концу их действия и истощения всего запаса, ракета остановится в той точке, у поверхности земли, с которой было начато поднятие. Способ поднятия строго тождествен со способом опускания; вся разница лишь в том, что скорости обратны в каждой точке пути.

Остановка в среде тяжести требует более работы и более взрывчатых веществ чем в среде свободной от тяготения; потому что в формулах 21 и 22 (q) должно быть больше, если применять ракету к среде тяжести.

Обозначив это большое отношение через (q₁), найдем на основании предыдущаго:

, откуда

Подставив (q1) вместо (q) в уравнение 22, получим.

23...q=q1

Здесь (М4) означает количество, или массу взрывчатых веществ, необходимую для поднятия с известной точки и возращения в ту-же точку при полной остановке ракеты и при полете ея в среде тяжести.

На основании последней формулы можем составить следующую таблицу, полагая, что =10, т. е., что давление взрывчатаго материала в 10 раз больше тяжести ракеты с остатком взрывчатых веществ. В этой таблице (V) выражает собственно работу ; — скорость же будет меньше, потому что часть этой работы ушла на поднятие в среде тяжести.

Табл. III. Для среды тяжести.

V в метр. 543 1.497 2.308 3.920 6.260 7.880 9.170 10.100 11.100 11.800

M2:M1 0,1 0,3 0,5 1,0 2 3 4 5 6 7

M4:M1 0,235 0,778 1,420 4,457 9,383 17,78 28,64 41,98 57,78 76,05

---

Среда тяжести. Наклонное поднятиe.

Хотя вертикальное движение ракеты как будто выгоднее, потому что при этом cкopее разсекается атмосфера и снаряд подымается на большую высоту; — но, с одной стороны, работа разсечения атмосферы, сравнительно с полною работою взрывчатых веществ, весьма незначительна, с другой, при наклонном движении, можно устроить постоянную обсерваторию, движущуюся за пределами атмосферы неопределенно долгое время вокруг земли, подобно ея луне. Кроме того и это главное — при наклонном полете утилизируется несравненно большая часть энергии взрыва, чем при вертикальном движении.

Разсмотрим сначала частный случай, — когда полет ракеты горизонтален.

Если через (R) обозначим величину равнодействующей горизонтальнаго ycкopения ракеты, через (р) ускорение от действия взрывания и через (g) ycкopeниe от силы тяжести, то имеем:

Кинетическая энергия, полученная снарядом чрез время (t), равна, на основании последней формулы:

где (t) есть время взрывания. Это и есть вся полезная работа, приобретенная ракетой. Действительно ракета нисколько не поднимется, если принять направление тяжести постоянным (что на практике только при небольшой траектории снаряда верно).

Работа-же взрывчатых веществ, приобретенная ракетой в среде, свободной от тяжести, равна:

Разделив полезную работу (25) на полную (26), получим утилизацию при горизонтальном полете ракеты:

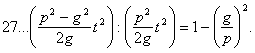
Сопротивление воздуха, как и прежде, пока в расчет не принимается.

Из последней формулы видно, что потеря работы, сравнительно с работою в среде, свободной от силы тяготения, выражается через Отсюда следует, что эта потеря гораздо меньше, чем при отвесном движении. Так напр., при потеря составит 1/100 т. е. один процент между тем как при вертикальном движении она выражалась через или равнялась 1/10 т. е. десяти процентам.

Вот таблица, где (В) есть угол иаклонения силы (р) к горизонту:

Горизонтальное движение ракеты.

p:g 1 2 3 4 5 10 100

Потеря 1 1:4 1:9 1:16 1:25 1:100 1:10 000

sиn β 1 1:2 1:3 1:4 1:5 1:10 1:100

β Градусы 90° 30 19,5 14,5 11,5 5,7 0,57

Теперь решим вопрос вообще, — при всяком наклонении равнодействующей (В). Горизонтальность траектории, или равнодействующей, как я уже говорил, невыгодна потому, что при таком движении снаряда страшно увеличивается его путь через атмосферу, a вместе с тем увеличивается и работа разсечения им воздуха.

Итак, будем помнить, что (α), или угол наклонения равнодейcтвyющей к вертикали, больше прямого угла, Имеем:

где (γ)= α+3 (тyпoй угол параллелограмма, по чертежу ). Далее: sin (α): sin (β): sin (γ) = р:g R1 и

Кинетическая работа выражается формулой 9, где (R) определяется согласно ypавнению 29. Вертикальное ускорение (R1) равнодействующей (R) равно; 79...R1=sin (α-90). R= -cos (α).R.

Следовательно работа поднятия снаряда будет равна:

где (t) есть время взрывания всего запаса взрывчатых веществ. Полная работа, приобретенная снарядом с среде тяжести, выразится:

Здесь за единицу работы принято поднятие снаряда на единицу высоты, в среде с ускорением (g). Если [α] 90°, напр. в случае поднятия снаряда, то (- cos α) есть величина положительная и обратно.

Работа в среде, свободной от тяжести, будет, равна.

(не забудем, что время (t) взрывания не зависит от сил тяготения).

Взяв отношение этих двух работ получим утилизацию энергии взрывчатых веществ, сравнительно с утилизациею их в среде лишенной тяжести; именно:

Выключая отсюда (R) по формуле 29, найдем:

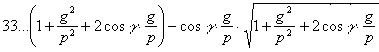
Формула 27 напр. есть только частный случай этой, в чем легко убедиться.

Сделаем сейчас же применение найденной формулы. Положим, что ракета летит в верх под углом в 14,5° к горизонту; синус этого угла составляет 0,25; это значит, что сопротивление атмосферы увеличивается в 4 раза сравнительно с сопротивлением ея при отвесном движении снаряда; ибо, приблизительно, сопротивление ея обратно пропорционально синусy угла наклона (α — 90°) траектории ракеты к горизонту.

85. Угол α = 90 + 14½ = 104½ °; соs α = — 0,25; зная (α), можем узнать и (β); действительно, найдем: sin β = sin α·; так, если = 0,1, то sin β = 0,0968, откуда β = 110°; cos γ = — 0,342.

Теперь, пo формуле 32, вычислим отилизацию в 0,966. Потеря составляет 0,034, или около 1/29,вернее, 3,4%.

Эта потеря в 3 раза меньше, чем при вертикальном движении. Результат недурной, если прнять еще во внимание, что сопротивление атмосферы и при наклонном движении (14½ °) , никак не более одного процента работы удаления снаряда от земли.

Для разных соображений предлагаем следующую таблицу. 1-й столбец показывает наклонение движения к горизонту, последний потерю работы; (β) есть отклонение направления давления взрывчатых веществ от линии действительнаго движения

Наклонное движение.

Градусы				утилизация	Потеря.
α — 90. 0 2 5 10 15 20 30 40 45 90	α. 90 92 95 100 105 110 120 130 135 180	β. 53/4 52/3 52/3 52/3 51/2 51/3 5 41/3 4 0	γ = α+β 952/3 972/3 1002/3 1052/3 1101/2 1151/3 125 1341/3 139 180	0,9900 0,9860 0,9800 0,9731 0,9651 0,9573 0,9426 0,9300 0,9246 0,9000	1:100 1:72 1:53 1:37 1:29 1:23,4 1:17,4 1:14,3 1:13,3 1:10

Для очень малых углов наклона (α — 90°), формулу 33 можно чрезвычайно упростить, заменив тригонометрическия величины их дугами и сделав другия упрощения.

Тогда получим следующее выражение для потери работы:

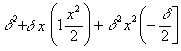где (δ) означает угол наклона движения (α — 90°), выраженный длиною его дуги, радиус который равен единице, — а (х) — отношение

Откидывая в последней формуле малыя высших порядков, получим для потери:

Можем положить.

δ = 0,02N, где 0,02 есть часть окружности, соответствующая почти одному градусу a (N) число этих новых градусов. Таким образом потеря работы, приблизительно выразится;

По этой формуле легко составим следующую таблицу, положив =0,1

N	0	0,5	1	2	3	4	5	6	10
Потеря	1/100	1/91	1/83	1/70	1/60	1/55	1/50	1/45	1/33

Отсюда видим, что даже для больших углов (до 10°) противоречие между этой таблицой и предыдущей, более точной, не велико.

---

Мы могли бы разсмотреть еще очень многое: работу тяготения, сопротивление атмосферы; мы совсем еще ничего не сказали о том как изследователь может пробыть продолжительное, даже неопределенно долгое время в среде, где нет следов кислорода; мы не упомянули о нагревании снаряда при кратковременном полете в воздухе, мы не дали даже общей картины полета и сопровождающих его крайне интересных явлений (теоретически); мы почти не указали на великия перспективы в случае осуществления дела, рисущияся нам пока еще в тумане; наконец, мы могли-бы начертать космическия кривыя движения ракеты в небесном пространстве.