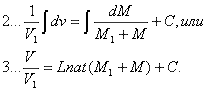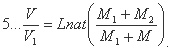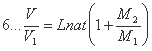вернёмся в библиотеку?

Если Вы не видите дореволюционных „ятей“, установите шрифт Palatino Linotype или читайте на современном

---

Дозволено цензурою СПБ. 31 мая 1903 года.

---

СОДЕРЖАНIЕ № 5.

---

ОТДѢЛЪ ПЕРВЫЙ.
1. Завѣтныя мысли. Проф. Д. Менделѣева. I. Вступленiе
2. Вопросы этики и вопросы хозяйства въ исторiи. Проф. Л. Брентано (пер. П. Берлина)
3. Изслѣдованiе мiровыхъ пространствъ реактивными приборами. К. Цiолковскаго
4. Нѣмецкая литература въ XIX столѣтiи. Мейера (пер. А. Филипповой).
5. Сенъ-Симонъ и сенъ-симонизмъ. (Окончанiе). X. Инсарова
6. Невидимые лучи свѣта. Проф. Д. А. Гольдгаммера
7. Литературные образы мнѣнiя: разсказы Куприна, Бунина, Серафимовича, Телешова и Юшкевича. Не страшное В. Короленки. „Чеховщина“; въ текущей русской литературѣ. О правдѣ и лжи, борьбѣ и раздумьѣ. Е. Аничкова
8. Загадка Шекспира въ трагедiи „Гамлетъ“. Тѣнь короля Гамлета. С. Москаленки
9. Философскiя письма: I. Творчество личности. М. Филиппова.
10. Трудовая теорiя цѣнности и ея критики. А. Финна
11. Научныя новости. (Подъ ред. проф. С. П. Глазенапа)
12. Обзоръ печати. В. Т — ца

ОТДѢЛЪ ВТОРОЙ.
13. Онъ и они. С. Бердяева
14. Барышня. (Драма). Стриндберга.
15. Cтиxoтвоpeнie H. З.
16.Хлѣбъ насущный. Клары Фиттигъ (пep. П. Гиберманъ). Въ приложенiи.

---

ОТДѢЛЪ ТРЕТIЙ.
17. Народный Университетъ. Лассаръ Конъ. Химiя обыденной жизни.

---

Изслѣдованiе мировыхъ пространствъ реактивными приборами

Небольшие аэростаты съ автоматически наблюдающими приборами, безъ людей, до сихъ поръ поднимались только до высоты, не большей 20 верстъ.

Трудность поднятiя въ высоту съ помощiю воздушныхъ шаровъ возрастаетъ чрезвычайно быстро съ увеличенiемъ этой высоты.

Положимъ, мы хотимъ, чтобы аэростатъ поднялся на высоту 27 километровъ и поднялъ грузъ въ 1 килограммъ (2,4 фунта). Воздухъ на высотѣ 27 килом. имѣетъ плотность около ¹/₅₀ плотности воздуха при обыкновенныхъ условiяхъ (760 мм. давленiя и 0° Цельсiя). Значитъ шаръ на такой высотѣ долженъ занять объемъ въ 50 разъ больший, чѣмъ внизу. У уровня же океана слѣдуетъ впустить въ него не менѣе 2 кубич. метровъ водорода, которые на высотѣ займутъ 100 куб. метровъ. При этомъ шаръ подниметъ грузъ въ 1 килограммъ, т. е. подниметъ автоматическiй приборъ, а самъ шаръ будетъ вѣсить килограммъ или около того.

Поверхность его оболочки, при дiаметрѣ въ 5,8 метра, составитъ не менѣе 103 кв. метровъ. Слѣдовательно каждый квадратный метръ матерiи, считая и пришитую къ ней сѣтку, долженъ вѣсить 10 граммовъ, или квадр. аршинъ будетъ вѣсить около 1-го золотника.

Кв. метръ этой писчей бумаги вѣситъ 100 граммовъ; вѣсъ же кв. метра папиросной бумаги составляетъ граммовъ 50. Такъ что даже папиросная бумага будетъ въ 5 разъ тяжелѣе той матерiи, которая должна быть употреблена на нашъ аэростатъ. Такая матерiя, въ примѣненiи къ аэростату, невозможна, потому что оболочка, сдѣланная изъ нея, будетъ рваться и сильно пропускать газъ.

Шары большихъ размѣровъ могутъ имѣть болѣе толстую оболочку. Такъ шаръ съ небывало большимъ дiаметромъ въ 58 метровъ будетъ имѣть оболочку, каждый квадратный метръ которой вѣситъ около 100 граммовъ, т. е. чуть тяжелѣе обыкновенной писчей бумаги. Подыметъ онъ 1000 килогр. груза, или 61 пудъ, что черезчуръ много для самопишущаго прибора.

Если ограничиться, при тѣхъ же громадныхъ размѣрахъ аэростата, подъемною силою въ 1 килограммъ, то оболочку можно сдѣлать раза въ 2 тяжелеѣ. Вообще, въ такомъ случаѣ, аэростатъ хотя и обойдется весьма дорого, но построенiе его нельзя считать дѣломъ невозможнымъ. Объемъ его на высотѣ 27 килом. составитъ 100.000 куб. метровъ, поверхность оболочки — 10.300 кв. метровъ.

А между тѣмъ какiе жалкiе результаты! Поднятiе на какiе-то 25 верстъ...

Что же сказать о поднятiи приборовъ на большую высоту! Размѣры аэростатовъ должны быть еще значительно больше, но не надо при этомъ забывать, что съ увеличенiемъ размѣровъ воздушнаго шара разрывающiя оболочку силы все болѣе и болѣе берутъ поревѣсъ надъ сопротивленiемъ матерiала.

Высота атмо- сферы въ ки- лометрахъ.	Температура по Цельсiю.	Плотность воздуха.
0 6 12 18 24 30 36 42 48 54,5	0 -30 -60 -90 -120 -150 -180 -210 -240 -272	1: 1:2 1:4,32 1:10,6 1:30,5 1:116 1:584 1:3900 1:28.000 0.

За предѣлы атмосферы поднятiе приборовъ, съ помощiю воздушнаго шара, разумѣется совсѣмъ немыслимо; изъ наблюденiй надъ падающими звѣздами видно, что предѣлы эти не простираются далѣе 200 — 300 километровъ.

Теоретически даже опредѣляютъ высоту атмосферы въ 54 километра, принимая въ основанiе расчета понiженiе температуры воздуха въ 5° Цельсiя на каждый километръ поднятiя, что довольно близко къ дѣйствительности, по крайней мѣрѣ для доступныхъ слоевъ атмосферы.

Выше приведена таблица высотъ, температуръ и плотностей воздуха, вычисленная мною на этомъ основанiи. Изъ нея очевидно, какъ быстро возрастают трудности поднятiя, съ увеличенiемъ его высоты.

Дѣлитель послѣдняго столбца и выражаетъ эту трудность устроенiя воздушнаго шара.

Перейдемъ къ другой идеѣ поднятiя, — съ помощiю пушечныхъ ядеръ.

На практикѣ, начальная быстрота ихъ движенiя не превышаетъ 1200 метровъ въ секунду. Такое ядро, пущенное вертикально, поднимется на высоту въ 73 километра, если поднятiе совершается въ безвоздушномъ пространствѣ. Въ воздухѣ, разумѣется, поднятiе много меньше, въ зависимости отъ формы и массы ядра.

При хорошей формѣ поднятiе можетъ достигать значительной величины, но помѣщать наблюдающiе приборы внутри ядра невозможно потому что они будутъ разбиты въ дребезги — или при возвращенiи ядра на землю, или при самомъ движенiи его въ пушечномъ стволѣ..

Опасность при движенiи ядра въ каналѣ меньше, но и эта опасность, для цѣлости аппаратовъ, громадна. Положимъ, для простоты что давленiе газовъ на ядро равномѣрно, вслѣдствiе чего, ускоренiе его движенiя въ секунду составляетъ (W) метровъ. Тогда тоже ускоpeнie получаютъ и всѣ предметы въ ядрѣ, принужденные совершать съ нимъ одно движенѣе. Отъ этого внутри ядра должна развиться относительная, кажущаяся тяжесть, равная гдѣ (g) есть ускоренiе земной тяжести у поверхности земли.

Длина пушки (L) выразится формулой

, гдѣ

(V) есть скорость, прiобрѣтаемая ядромъ по выходѣ изъ жерла.

Изъ формулы видно, что (W), а слѣдовательно и приращенiе относительной тяжести въ ядрѣ уменьшается съ увеличенiемъ длины пушки, при постоянномъ (V); т. е. чѣмъ длиннѣе пушка, тѣмъ приборы безопаснѣе во время выталкиванiя ядра. Но и при очень длинной, неосуществимой на дѣлѣ пушкѣ, кажущаяся въ ядрѣ тяжесть, при ускоряющемся его движенiи въ пушечномъ каналѣ, настолько велика, что нѣжно устроенные аппараты едва ли могутъ перенести ее безъ порчи. Тѣмъ болѣе невозможно послать въ ядрѣ что нибудь живое, если бы въ этомъ случилась надобность.

Итакъ допустимъ, что построена пушка ну хоть въ 300 метровъ высоты. Пусть она расположена вдоль башни Эйфеля, которая, какъ извѣстно, имѣетъ такую же высоту, и пусть ядро равномѣрнымъ давленiемъ газовъ получаетъ, при выходѣ изъ жерла, скорость, достаточную для поднятiя за предѣлы атмосферы, напр. для поднятiя на 300 килом. отъ земной поверхности. Тогда потребную для этого скорость (V) вычислимъ по формулѣ V = , гдѣ (h) высота поднятiя; — (получимъ около 2450 м. въ 1 секунду). Изъ двухъ послѣднихъ формулъ, исключая (V), найдемъ; <

/table> выражаетъ относительную, или кажущуюся тяжесть въ ядрѣ. По формулѣ найдемъ, что оно ровно 1001.

Слѣдовательно тяжесть всѣхъ приборовъ въ ядрѣ должна увеличиться въ 1000 разъ слишкомъ, т. е. предметъ вѣсомъ въ одинъ фунтъ испытываетъ отъ кажущейся тяжести давленiе въ 1000 фунтовъ или 25 пудовъ. Едва ли какой физическiй приборъ выдержитъ подобное давленѣе.

Чтобы не ввести кого нибудь въ заблужденiе словомъ „относительная или кажущаяся тяжесть“, скажу, что я тутъ подразумѣваю силу, зависящую отъ ускоряющагося движенiя тѣла (напр. ядра); она появляется также и при равномѣрномъ движенiи тѣла, если только это движенiе криволинейно, и называется тогда центробѣжной силой. Вообще она появляется всегда на тѣлѣ или въ тѣлѣ, если только на одно это тѣло дѣйствуетъ какая либо механическая сила, нарушающая движенiе тѣла по инерцiи.

Относительная тяжесть существуетъ до тѣхъ поръ, пока существуетъ рождающая ее сила: прекращается послѣдняя — исчезаетъ безслѣдно и относительная тяжесть. Если я называю эту силу тяжестью, то только потому, что ея временное дѣйствiе совершенно тождественно съ дѣйствiемъ силы тяготѣнiя. Какъ тяготѣнiю подвержена каждая матерiальная точка тѣла, такъ и относительная тяжесть рождается въ каждой частицѣ тѣла, заключеннаго въ ядрѣ происходитъ это потому, что кажущаяся тяжесть зависитъ отъ инерцiи, которой одинаково подвержены всѣ матерiальныя части тѣла.

Итакъ, приборы внутри ядра сдѣлаются тяжелѣе въ 1001 разъ. Если бы даже при этомъ страшномъ, хотя и кратковременномъ (0,24 секунды) усиленiи относительной тяжести и удалось ихъ сохранить въ цѣлости, то все же найдется много другихъ препятствiй для употребленiя пушекъ въ качествѣ посылателей въ небесное пространство.

Прежде всего трудность ихъ построенiя даже въ будущемъ; далѣе — громадная начальная скорость ядра; дѣйствительно, въ нижнихъ густыхъ слояхъ атмосферы, скорость ядра много потеряетъ вслѣдствiе сопротивленiя воздуха; потеря же скорости сильно сократитъ и величину поднятiя ядра; затѣмъ трудно достигнуть равномѣрнаго давленiя газовъ на ядро во время его движенiя въ стволѣ, отъ чего усиленiе тяжести будетъ много болѣе, чѣмъ мы вычислили (1001); наконецъ, безопасное возвращенiе ядра на землю болѣе, чѣмъ сомнительно.

Реактивный приборъ — „ракета“.

Впрочемъ, одного громаднаго усиленiя тяжести совершенно достаточно, чтобы оставить мысль о примѣненiи пушекъ къ нашему дѣлу.

Вмѣсто ихъ, или аэростата, въ качествѣ изслѣдователя атмосферы, предлагаю реактивный приборъ, т.е. родъ ракеты, но ракеты грандiозной и особеннымъ образомъ устроенной. Мысль не новая, но вычисленiя, относящiяся къ ней, даютъ столь замѣчательные результаты что умолчать о нихъ было бы большимъ грѣхомъ.

Эта моя работа далеко не разсматриваетъ всѣхъ сторонъ дѣла и совсѣмъ не рѣшаетъ его съ практической стороны — относительно осуществимости; но въ далекомъ будущемъ уже виднѣются сквозь туманъ перспективы до такой степени обольстительныя и важныя, что о нихъ едва ли теперь кто мечтаетъ.

Представимъ себѣ такой снарядъ: металлическая продолговатая камера (формы наименьшаго сопротивленiя), снабженная свѣтомъ, кислородомъ, поглотителями углекислоты, мiазмовъ и другихъ животныхъ выдѣленiй, — предназначена не только для храненiя разныхъ физическихъ приборовъ, но и для управляющаго камерой разумнаго существа (будемъ разбирать вопросъ по возможности шире). Камера имѣетъ большой запасъ веществъ, которыя при своемъ смѣшенiи тотчасъ же образуютъ взрывчатую массу. Вещества эти правильно и довольно равномѣрно взрываясь въ опредѣленномъ для того мѣстѣ, текутъ въ видѣ горячихъ газовъ по расширяющимся къ концу трубамъ, вродѣ рупора или духового музыкальнаго инструмента. Трубы эти расположены вдоль стенокъ камеры, по направленiю ея длины. Въ одномъ узкомъ концѣ трубы совершается смѣшенiе взрывчатыхъ веществъ: тутъ получаются сгущенные и пламенные газы. Въ другомъ, расширенномъ ея концѣ они, сильно разрѣдившись и охладившись отъ этого, вырываются наружу, черезъ раструбы, съ громадною относительною скоростью.

Понятно, что такой снарядъ, какъ и ракета, при извѣстныхъ условiяхъ, будетъ подниматься въ высоту.

Необходимы автоматическiе приборы, управляющiе движенiемъ ракеты (такъ будемъ мы иногда называть нашъ приборъ) и силою взрыванiя по заранѣе намѣченному плану.

Схематическiй видъ ракеты.* Оба жидкихъ газа раздѣлены перегородкой. (А) есть мѣсто смѣшенiя газовъ и взрыванiя ихъ. (В)-вылетъ сильно разрѣженныхъ и охлажденныхъ паровъ. Труба АВ окружена кожухомъ съ быстро циркулирующей въ немъ металлической жидкостью.

*Рисунка в статье нет-Хл

Если равнодѣйствующая силъ взрыванiя не проходить точно черезъ центръ инерцiи снаряда, то снарядъ будетъ вращаться и слѣдовательно никуда не будетъ годится. Добиться же математической точности въ этомъ совпаденiи совершенно невозможно, потому что какъ центръ инерцiи не можетъ не колебаться вслѣдствiе движенiя заключенныхъ въ снарядѣ веществъ, такъ и направленiе въ пушкѣ равнодѣйствующей, силъ давленiя газовъ не можетъ имѣть математически-неизмѣнное направленiе. Въ воздухѣ еще можно направлять снарядъ рулемъ, подобнымъ птичьему, но что вы сдѣлаете въ безвоздушномъ пространстве, гдѣ эфиръ едва-ли представитъ какую-либо замѣтную опору?

Дѣло въ томъ, что если равнодѣйствующая по возможности близка къ центру инерцiи снаряда, то вращенiе его будетъ довольно медленно. Но едва только оно начинается, мы перемѣщаемъ какую-нибудь массу внутри снаряда до тѣхъ поръ, пока происходящее отъ этого перемѣщенiе центра инерцiи не заставитъ снарядъ уклоняться въ противоположную сторону. Такимъ образомъ, сдѣдя за снарядомъ и перемѣщая внутри его небольшую массу, достигнемъ колебанiя снаряда то въ ту, то въ другую сторону, общее же направленiе дѣйствiя взрывчатыхъ веществъ и движенiя снаряда изменяться не будетъ.

Можетъ быть ручное управленiе движенiемъ снаряда окажется не только затруднительнымъ, но и прямо практически невозможнымъ. Въ такомъ случаѣ слѣдуетъ прибѣгнуть къ автоматическому управленiю.

Основанiя для таковаго, послѣ сказаннаго, понятны.

Притяженiе земли не можетъ быть тутъ основной силой для регулированiя, потому что въ ядрѣ будетъ только относительная тяжесть съ ускоренiемъ (W), направленiе которой совпадаетъ съ относительнымъ направленiемъ вылетающихъ взрывчатыхъ веществъ или прямо противоположно направленiю равнодѣйствующей ихъ давленiя. А такъ какъ это направленiе меняется съ поворачиванiемъ ядра и пушки, то тяжесть эта, какъ направитель регулятора, не годится.

Возможно употребить для этой цѣли магнитную стрѣлку, или силу солнечныхъ лучей, сосредоточенныхъ съ помощiю двояко-выпуклаго стекла. Каждый разъ, когда ядро съ пушкой поворачивается, маленькое и яркое изображенiе солнца мѣняетъ свое относительное положенie въ ядрѣ, что можетъ возбуждать расширенiе газа, давленiе, электрическiй токъ и движенiе массы, возстановляющей опредѣленное направленiе пушки, при которомъ свѣтлое пятно падаетъ въ нейтральное, такъ сказать, нечувствительное мѣсто механизма.

Автоматически подвигаемыхъ массъ должно быть двѣ.

Основною для регулятора направленiя ядра также можетъ служить небольшая камера съ двумя быстро вращающимися въ разныхъ плоскостяхъ кругами. Камера привѣшена такъ, что положенiе или, точнѣе, направленiе ея не зависитъ отъ направленiя пушки. Когда пушка поворачивается, камера, въ силу инерцiи, пренебрегая тренiемъ, сохраняетъ прежнее абсолютное направленiе (относительно звѣздъ); это свойство проявляется въ высшей степени при быстромъ вращенiи камерныхъ дисковъ.

Прицѣпленныя къ камерѣ тонкiя пружинки, при поворачиванiи пушки, мѣняютъ въ ней свое относительное положенiе, что можетъ служить причиною возникновенiя тока и передвиженiя регулирующихъ массъ.

Наконецъ, поворачиванiе конца раструба также можетъ служить средствомъ сохраненiя опредѣленнаго направленiя снаряда.

Преимущества ракеты.

Прежде чѣмъ излагать теорiю ракеты или подобнаго ей реактивнаго прибора, попытаюсь заинтересовать читателя преимуществами ракеты передъ пушкой съ ея ядромъ.

а) Аппаратъ нашъ, сравнительно съ гигантской пушкой, легокъ, какъ перышко; b) онъ относительно дешевъ и сравнительно легко осуществимъ; с) давленiе взрывчатыхъ веществъ, будучи довольно равномѣрнымъ, вызываетъ равномѣрно-ускоряющееся движенiе ракеты, которое развиваетъ относительную тяжесть; величиною этой временной тяжести мы можемъ управлять по желанiю, т. е., регулируя силу взрыва, мы въ состоянiи сдѣлать ее произвольно мало или много превышающей обыкновенную земную тяжесть. Если продположимъ, для простоты, что сила взрыва, понемногу уменьшаясь, пропорцiональна массѣ снаряда, сложенной съ массою оставшихся невзорванными взрывчатыхъ веществъ, — то ycкоpeнie снаряда, а слѣдовательно и величина относительной тяжести будутъ постоянны. Итакъ, въ ракетѣ могутъ безопасно, въ отношенiи кажущейся тяжести, отправиться не только измѣрительные приборы, но и люди; тогда какъ въ пушечномъ ядрѣ, даже при огромной, небывалой пушкѣ, величиною съ башню Эйфеля, относительная тяжесть увеличивается въ 1001 разъ. d). Еще не малое преимущество ракеты: скорость ея возрастаетъ въ желаемой прогрессiи и въ желаемомъ направленiи; она можетъ быть постоянной и можетъ равномѣрно уменьшаться, что дастъ возможность безопаснаго спуска на планету. Все дѣло въ хорошемъ регуляторѣ взрыванiя. е) При началѣ поднятiя, пока атмосфера густа и сопротивленiе воздуха при большой скорости огромно, ракета двигается сравительно не быстро и потому мало теряетъ отъ сопротивленiя среды и мало нагрѣвается.

Скорость ракеты, естественнымъ образомъ, лишь медленно возрастаетъ; но затѣмъ, по мѣрѣ поднятiя въ высоту и разрѣженiя атмосферы, она можетъ искусственно возрастать быстрѣе; наконецъ, въ безвоздушномъ пространствѣ, эта быстрота возрастанiя можетъ быть еще усилена. Такимъ путемъ мы потратимъ „minimum” работы на преодолѣнiе сопротивленiя воздуха.

Ракета въ средѣ, свободной отъ тяжести и атмосферы.

Сначала разсмотримъ дѣйствiе взрыва въ средѣ, свободной отъ тяжести и окружающей матерiи, т. е. атмосферы. Относительно послѣдней мы беремся только разобрать ея сопротивленiе движенiю снаряда, но не движенiю вырывающихся стремительно паровъ. Влiянiе атмосферы на взрывъ не совсѣмъ ясно: съ одной стороны оно благопрiятно, потому что вырывающiяся вещества имѣютъ въ окружающей матерiальной средѣ нѣкоторую опору, которую они, при своемъ движенiи, увлекаютъ и такимъ образомъ способствуютъ увеличенiю скорости ракеты; но съ другой стороны, та же атмосфера, своей плотностью и упругостью мѣшаетъ расширенiю газовъ далѣе извѣстнаго предѣла, отъ чего взрывчатыя вещества не прiобрѣтаютъ той скорости, которую они могли бы прiобрѣсти, взрываясь въ пустотѣ. Это послѣднее влiянiе неблагопрiятно, потому что приращенiе скорости ракеты пpoпopцioнально скорости отбрасываемыхъ продуктовъ взрыва.

Массу снаряда со всѣмъ содержимымъ, кромѣ запаса взрывчатыхъ веществъ обозначимъ черезъ M₁; полную массу послѣднихъ черезъ М₂; наконецъ, перемѣнную массу взрывчатыхъ веществъ, оставшихся невзорванными въ снарядѣ въ данный моментъ — черезъ М.

Такимъ образомъ, полная масса ракеты, при началѣ взрыва будетъ равна (M₁+М₂); спустя же нѣкоторое время, она выразится перемѣнною величиною (M₁+M); наконецъ, пo окончанiи взрыванiя, — постоянной M₁

Чтобы ракета получила наибольшую скорость, необходимо чтобы отбрасыванiе продуктовъ взрыва совершалось въ одномъ направленiи относительно звѣздъ. А для этого нужно, чтобы ракета не вращалась; а чтобы она не вращалась, надо чтобы равнодѣйствующая взрывающихъ силъ, проходящая черезъ центръ ихъ давленiя, проходила въ то же время и черезъ центръ инерцiи всей совокупности летящихъ массъ.

Вопросъ, какъ этого достигнуть на практикѣ, мы уже слегка разобрали.

Итакъ, предполагая такое наивыгоднѣйшее отбрасыванiе газовъ въ одномъ направленiи, получимъ слѣдующее дифференцiальное уравнeнie, на основанiи закона о постоянствѣ количества движенiя:

1...dV(M₁+M)=V₁.dM.

Здѣсь dM есть безконечно-малый отбросокъ взрывчатаго вещества, вырывающагося изъ пушечнаго раструба съ постоянною относительно ракеты скоростью (V₁)

Я хочу сказать, что относительная скорость (V₁) вырывающихся элементовъ, при одинаковыхъ условiяхъ взрыва, одна и та же во все время взрыванiя, — на основанiи закона относительныхъ движенiй; (dv) есть приращенiе скорости (V) движенiя ракеты вмѣстѣ съ оставшимися нетронутыми взрывчатыми матерiалами; приращенiе это (dV) совершается, благодаря отбрасыванiю элемента (dM) со скоростiю (V₁). Опредѣленiемъ послѣдней мы займемся въ своемъ мѣстѣ.

Разделяя перемѣнныя величины въ уравненiи 1 и интегрируя, получимъ:

Тутъ С есть постоянное. Когда М=М₂, т. е. до взрыванiя, V=0; на этомъ основанiи найдемъ:

4... C= — Lnat (M₁+M2); *)

)* (Lnat) есть натуральный логари¬мъ
стало быть

Знаки обѣихъ частей уравненiя обратные, потому что скорости V и V₁ противоположны по направленiю.

Наибольшая скорость снаряда получится, когда М=0, т. е. когда весь запасъ (М₂) взорванъ; тогда получимъ, полагая въ предыдущемъ уравненiи M=0:

Отсюда мы видимъ, что скорость (V) снаряда возрастаетъ неограниченно съ возрастанiемъ количества (М₂) взрывчатыхъ веществъ. Значить, запасаясь разными количествами ихъ, при разныхъ путешествiяхъ, мы получимъ самыя разнообразныя окончательныя скорости. Изъ уравненiя 6 также видно, что скорость ракеты, по израсходованiи опредѣленнаго запаса взрывчатаго вещества, не зависитъ отъ быстроты или неравномѣрности взрыванiя, лишь бы частицы отбрасываемаго матерiала двигались съ одной и тою же скоростью (V1) относительно ядра.

Однако, съ увеличенiемъ запаса (М₂), скорость (V) ракеты возрастаетъ все медленнѣе и медленнѣе, хотя и безгранично. Приблизительно, она возрастаетъ, какъ логари¬мъ отъ увеличенiя количества взрывчатыхъ запасовъ (М₂), (если М₂ велико въ сравненiи съ М₁ т. е. масса взрывчатыхъ веществъ въ нѣсколько разъ больше массы снаряда).

Дальнѣйшiя вычисленiя будутъ интересны, когда мы опредѣлимъ (V₁), т. е. относительную и окончательную скорость взорваннаго элемента.

Такъ какъ газъ или паръ, при оставленiи пушечнаго раструба, весьма разрежается и охлаждается (при достаточной длинѣ трубы) — даже обращается въ твердое состоянiе, въ пыль, которая мчится съ страшною быстротою, — то можно принять, что вся энергiя горѣнiя, или химическаго соединенiя, при взрыванiи, обращается въ движенiе продуктовъ горѣнiя, или въ кинетическую энергiю. Въ самомъ дѣлѣ, представимъ себѣ опредѣленное количество газа, расширяющагося въ пустотѣ, безъ всякихъ приборовъ: онъ будетъ во всѣ стороны расширяться и вслѣдствiе этого охлаждаться до тѣхъ поръ, пока не превратится въ капли жидкости, или въ туманъ.

Туманъ этотъ обращается въ кристаллики, но уже не отъ расширенiя, а отъ испаренiя и лучеиспусканiя въ мiровое пространство.

Расширяясь, газъ выдѣлитъ всю свою явную и отчасти скрытую энергiю, которая превратится въ концѣ концевъ въ быстрое движенiе кристалликовъ, направленное во всѣ стороны, такъ какъ газъ расширялся свободно во всѣ стороны.

Если же его заставить расширяться въ резервуарѣ съ трубой, то труба направитъ движенiе газовыхъ молекулъ по определенному направленiю, чѣмъ мы и пользуемся для нашихъ цѣлей, т. е. для движенiя ракеты.

Какъ будто энергiя движенiя молекулъ превращается въ кинетическое движенiе до тѣхъ поръ, пока вещество сохраняетъ газообразное или парообразное состоянiе. Но это не совсѣмъ такъ. Дѣйствительно, часть вещества можетъ обратиться въ жидкое состоянiе; но при этомъ выдѣляется энергiя (скрытая теплота парообразованiя), которая передается оставшейся парообразной части матерiи и замедлитъ на некоторое времѣ переходъ ея въ жидкое состоянiе. Подобное явленiе мы видимъ въ паровомъ цилиндрѣ, когда паръ работаетъ собственнымъ расширенiемъ, выходъ же изъ парового котла въ цилиндръ запертъ. Тогда, при какой бы температурѣ не былъ паръ, часть eгo обращается въ туманъ, т.е. жидкое состоянiе, другая же часть продолжаетъ сохранять парообразное состоянiе и работать, заимствуя скрытую теплоту сгустившихся въ жидкость паровъ.

Итакъ, энергiя молекулярная будетъ превращаться въ кинетическую, по крайней мѣрѣ, до состоянiя жидкаго. Когда вся масса обратится въ капли, превращенiе въ кинетическую энергiю почти прiостановится, потому что пары жидкихъ и твердыхъ тѣлъ, при низкой температурѣ, имѣютъ черезчуръ незначительную упругость и использованiе ихъ на практикѣ затруднительно, такъ какъ потребует огромныхъ трубъ.

Однако нѣкоторая незначительная часть указанной нами энергiи пропадетъ для насъ, т. е. не превратится въ кинетическую энергiю, благодаря тренiю о трубу и лучеиспусканiю теплоты нагретыми ея частями. Впрочемъ, труба изъ красной мѣди можетъ быть окружена кожухомъ, въ которомъ циркулируетъ какой нибудь жидкiй металлъ; онъ передастъ жаръ весьма нагрѣтой части одного конца трубы другой ея части, охлажденной вслѣдствiе сильного разрѣженiя паровъ. Такимъ образомъ и эта потеря, отъ лучеиспусканiя и теплопроводности, можетъ быть утилизирована или сдѣлана очень незначительной. Въ виду кратковременности взрыванiя, продолжающагося въ крайнихъ случаяхъ отъ 2 до 5 минутъ, потеря отъ лучеиспусканiя и безъ всякихъ приспособленiй незначительна; циркуляцiя же металлической жидкости въ кожухѣ, окружающемъ трубы, необходима для другой цѣли: для поддержанiя трубъ при одной и той же невысокой температурѣ, т. е. для сохраненiя крѣпости трубы. Несмотря на это, возможно, что часть ея будетъ расплавлена, окислена и унесена вмѣстѣ съ газами и парами. Можетъ быть, для избежанiя этого, внутреннюю часть трубы будутъ выкладывать какимъ-нибудь особеннымъ огнеупорнымъ матерiаломъ, углеродомъ, известью (СаО.) или чѣмъ-нибудь инымъ. Хотя часть углерода при этомъ и сгоритъ, но крѣпость металлической пушки, мало нагрѣтой, пострадать отъ этого не можетъ.

Газообразный же продуктъ горѣнiя углерода — углекислота только усилитъ поднятiе ракеты. Можетъ быть употребленъ будетъ родъ тигельнаго матерiала — какая-нибудь смѣсь веществъ. Во всякомъ случаѣ, не я рѣшу этотъ вопросъ, какъ и множество другихъ, относящихся къ нашимъ реактивнымъ приборамъ.

Во многихъ случаяхъ я принужденъ лишь гадать или предполагать. Я нисколько не обманываюсь и отлично знаю, что не только не рѣшаю вопроса во всей полноте, но что остается поработать надъ нимъ въ 100 разъ больше, чѣмъ я поработалъ. Моя цѣль возбудить къ нему интересъ, указавъ на великое значенiе его въ будущемъ и на возможность его рѣшенiя...

Для уменьшенiя протяженiя, занимаемаго трубами, при той же длинѣ ихъ, можно завивать ихъ кольцами или змѣевикомъ, окруженнымъ, для сохраненiя умѣренной и равномѣрной температуры, хорошо проводящей тепло и быстро циркулирующей жидкостью.

Въ настоящее время обращенiе водорода и кислорода въ жидкость не представляетъ особенныхъ затрудненiй. Жидкости эти должны быть раздѣлены перегородкой. Температура ихъ весьма низкая; поэтому ими полезно окружать или кожухи съ циркулирующимъ металломъ, или непосредственно самыя пушки.

Опытъ покажетъ какъ сдѣлать лучше. Но въ послѣднемъ случаѣ для трубъ мѣдь уже не годится, потому что она при очень низкой температурѣ дѣлается хрупкой и, вѣроятно, теряетъ свою вязкость. Нѣкоторые же металлы, напротивъ, дѣлаются крѣпче отъ охлажденiя; вотъ такiе то металлы и нужно тогда употребить, напр., желѣзо. Не помню хорошо, но какiе то опыты, надъ сопротивленiемъ, кажется, желѣза, въ жидкомъ воздухѣ, указали, что вязкость его при этой низкой температурѣ увеличивается чуть ли не въ десятки разъ. За достовѣрность не ручаюсь, но опыты эти въ примѣненiи къ нашему дѣлу, заслуживаютъ глубочайшаго вниманiя. (Почему бы не охлаждать такимъ образомъ и обыкновенныя пушки, прежде чѣмъ изъ нихъ стрѣлять; вѣдь жидкѣй воздухъ теперь такая обыкновенная вещь).

Жидкiй кислородъ и такой же водородъ, выкачиваемые изъ своихъ резервуаровъ, въ извѣстномъ отношенiи, въ узкое начало трубы и соединяясь тутъ понемногу, могутъ дать прекрасный взрывчатый матерiалъ. Получаемый при химическомъ соединенiи этихъ жидкостей водяной паръ, при страшно высокой температурѣ, будетъ расширяться, подвигаясь къ концу, или устью трубы до тѣхъ поръ, пока не охладится до того, что обратится въ жидкость, несущуюся въ видѣ тончайшаго тумана по направленiю длины трубы, къ ея выходу (раструбу).

Водородъ и кислородъ въ жидкомъ видѣ, прежде чѣмъ попасть въ пушку, пройдутъ по особому кожуху, вдоль ея поверхности, охладятъ ее, сами нагрѣются и тогда уже попадаютъ въ пушку и взрываются; такимъ образомъ, энергiя тепла, уходящаго путемъ теплопроводности и лучеспусканiя изъ пушки опять въ нее возвращается, чтобы обратиться въ энергiю поступательнаго движенiя пара или тумана.

Водородъ и кислородъ, въ газообразномъ состоянiи, соединяясь для образования одного килограмма воды, развиваютъ 3825 калорiй. Подъ словомъ „калорiя" мы тутъ подразумѣваемъ количество теплоты, потребное для нагрѣванiя на 1° Цельсiя одного килограмма воды.

Количество это (3825) у насъ будетъ немного меньше, разъ кислородъ и водородъ находятся въ жидкомъ состоянiи, а не въ газообразномъ, къ каковому относится данное нами число калорiй. Въ самомъ дѣлѣ, жидкости, во-первыхъ, надо нагрѣть, во-вторыхъ обратить въ газообразное состоянiе, на что расходуется нѣкоторая энергiя. Въ виду незначительной величины этой энергiи, сравнительно съ энергiей химической, мы оставимъ наше число безъ умаленiя.

Принимая механическiй эквивалентъ теплоты въ 424 килограмметра, найдемъ, что 3825 калорiй соотвѣтствуютъ работѣ въ 1.621.800 килограмметровъ; этого достаточно дли поднятiя продуктовъ взрыва, т. е. одного килограмма вещества, на высоту 1.622 киллометра отъ поверхности земного шара, предполагая силу тяжести постоянной. Эта работа, превращенная въ движенiе, соотвѣтствуетъ работѣ одного килограмма массы, движущейся со скоростью 5.700 метровъ въ 1 секунду. Я не знаю ни одной группы тѣлъ, которыя, при своемъ химическомъ соединенiи, выдѣляли бы, на единицу массы полученнаго продукта, такое огромное количество энергiи. Kpoмѣ того, нѣкоторыя другiя вещества, соединяясь, не образуютъ летучихъ продуктовъ, что для насъ совсѣмъ не годится.

Такъ кремнiй, сгорая въ кислородѣ (Si+O2= Si O2), выдѣляетъ огромное количество тепла, именно 3654 калорiи на единицу массы полученнаго продукта (Si O2), но къ сожалѣнiю образуются трудно-летучiя тѣла.

Принявъ жидкiй кислородъ и водородъ за матерiалъ, наиболѣе пригодный для взрыванiя, я далъ число для выраженiя ихъ взаимной химической энергiи, приходящейся на единицу массы полученнаго продукта (Н2 О), нѣсколько большее истиннаго, такъ какъ вещества, соединяющiяся въ ракетѣ, должны находиться въ жидкомъ, а не въ газообразномъ состоянiи, и кромѣ того при очень низкой температурѣ.

Считаю не лишнимъ тутъ утѣшить читателя, что не только на эту энергiю (3825 кал.), но и на несравненно большую мы можемъ надѣяться въ будущемъ, когда можетъ быть найдутъ возможнымъ осуществить наши недовольно разработанныя еще мысли. Въ самомъ дѣлѣ, разсматривая количество энергiи, получаемыя отъ химическихъ процессовъ разнообразныхъ веществъ, замѣчаемъ въ общемъ, не безъ исключенiй конечно, что количество энергiи, приходящейся на единицу массы продуктовъ соединенiя, зависитъ отъ атомныхъ вѣсовъ (въ большинствѣ случаевъ) соединяющихся простыхъ тѣлъ: чѣмъ меньше атомные вѣса тѣлъ, тѣмъ болѣе выдѣляется при соединенiи ихъ тепла. Такъ, при образованiи сѣрнистаго газа (SО2), образуется только 1250 калорiй, а при образованiи окиси мѣди (СиО) — только 546 калорiй; между тѣмъ какъ уголь, при образованiи углекислоты (СО2), выдѣляетъ на единицу ея массы 2204 калорiи. Водородъ съ кисдородомъ, какъ мы видѣли, выдѣляютъ еще больше (3825). Для оцѣнки этихъ данныхъ, къ примѣненiю въ высказанной мною идеи, напомню тутъ величину атомныхъ вѣсовъ приводимыхъ элементовъ: водородъ = 1; кислородъ = 16; углородъ = 12; сѣра = 32; кремнiй = 28; мѣдь = 63.

Конечно, можно привести и много исключенiй изъ этого правила, но въ общемъ оно справедливо. Дѣйствительно, если мы вообразимъ рядъ точекъ, абсциссы которыхъ выражаютъ сумму (или произведенiе) атомныхъ вѣсовъ соединяющихся простыхъ тѣлъ, а ординаты соотвѣтствующую энергiю химическаго соединенiя, то, проведя черезъ точки (по возможности ближе къ нимъ) плавную кривую, увидимъ непрерывное уменьшенiе ординатъ по мѣрѣ увеличенiя абсциссъ, чѣмъ и доказывается нашъ взглядъ.

Поэтому, если когда-нибудь такъ называемыя простыя тѣла окажутся сложными и ихъ разложатъ на новые элементы, то атомные вѣса послѣднихъ должны быть меньше извѣстныхъ намъ простыхъ тѣлъ. Новооткрытые элементы, по предыдущему, при своемъ соединенiи, должны выдѣлять при своемъ соединенiи несравненно большое количество энергiи, чѣмъ тѣла, считаемыя теперь условно простыми и имѣющiя сравнительно большой атомный вѣсъ.

Объ iонахъ, или подъатомахъ давно уже высказывались и даже думаютъ, что условные элементы разлагаются на эти ioны подъ влiянiемъ солнечнаго свѣта.

Самое существование эфира съ его почти бозпредѣльною упругостью и громадною скоростью его атомовъ, указывает на безпредѣльно малый атомный вѣсъ этихъ атомовъ и безпредѣльную энергiю въ случаѣ ихъ химическаго соединенiя.

Какъ бы то ни было, но пока для V₁ (см. 15 и 16) мы не можемъ принять болѣе 5700 метровъ въ 1 секунду. Но со временемъ кто знаетъ, можетъ быть это число увеличится въ несколько разъ.

Принимая 5700 метровъ, можемъ по формулѣ 16 вычислить не только отношенiе скоростей , но и абсолютную величину окончательной (наибольшей) скорости (V) снаряда въ зависимости отъ отношенiя

Изъ формулы 6 видно, что масса ракеты со всѣми пассажирами и всѣми аппаратами (М₁) можетъ быть произвольно велика и скорость (V) снаряда отъ этого нисколько не потеряетъ, лишь бы запасъ взрывчатыхъ веществъ (М₂) возрасталъ пропорцiонально возрастанiю массы (М₁) ракеты. Итакъ, всевозможной величины снаряды, съ любым числомъ путешественниковъ, могутъ прiобрѣтать скорости желаемой величины. Впрочемъ возрастанiе скорости ракеты сопровождается, какъ мы видѣли, несравненно быстрѣйшимъ возрастанiемъ массы (М₂) взрывчатыхъ воществъ. Поэтому насколько легко и возможно увеличенiе массы поднимающагося въ небесное пространство снаряда, настолько затруднительно увеличенiе его скорости.

Изъ уравненiя 6 получимъ следующую таблицу:

, тутъ

		Секундная скорость (V) в метрах			Секундная скорость (V) в метрах
0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6	0,095 0,182 0,262 0,336 0,405 0,693 1,098 1,386 1,609 1,792 1,946	543 1.037 1.493 1.915 2.308 3.920 6.260 7.880 9.170 10.100 11.100	7 8 9 10 19 20 30 50 100 193 Безконечно.	2,079 2,197 2,303 2,398 2,996 3,044 3,434 3,932 4,615 5,268	11.800 12.500 13.100 13.650 17.100 17.330 19.560 22.400 26.280 30.038 Безконечно.

Изъ нея усматриваемъ, что скорости, получаемыя реактивнымъ путемъ далеко не малы. Такъ при массѣ взрывчатыхъ веществъ, въ 193 раза превышающей вѣсъ (M₁) снаряда (ракеты), скорость его, по окончанiи взрыванiя и израсходованiя всего запаса (М₂), равна скорости движенiя земли вокругъ солнца. Не думайте, что такая громадная масса взрывчатаго матерiала требуетъ для своего сохраненiя громаднаго количества крѣпкаго матерiала для сосудовъ, содержащихъ взрывчатые элементы. Дѣйствительно, водородъ и кислородъ въ жидкомъ видѣ только тогда обнаруживаютъ высокое давленiе, когда сосуды, содержащiе ихъ, заперты, т. е. когда самые газы, влiянiемъ окружающихъ сравнительно теплыхъ тѣлъ, нагрѣваются. У насъ же эти ожиженные газы должны имѣть свободный выходъ въ трубу (помимо постояннаго притока ихъ туда въ жидкомъ видѣ), гдѣ они, соединяясь химически, взрываютъ. Непрерывное и быстрое теченiе газовъ, соотвѣтствующее испаренiю жидкостей, охлаждаетъ эти послѣднiя до того, что онѣ, своими парами, не производятъ почти никакого давленiя на окружающiя ихъ стѣнки. Итакъ, для сохраненiя элементовъ взрыва, не требуется на сосудъ большой массы вещества.

Когда запасъ взрывчатаго вещества равенъ массѣ ракеты 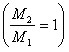, то скорость послѣдней чуть не вдвое болѣе той, которая нужна, чтобы камню или пушечному ядру, пущенному „селенитами“ съ поверхности нашей луны, удалиться отъ нея навсегда и сдѣлаться спутникомъ земли, второй луной.

Эта скорость (3920 метровъ въ секунду) почти достаточна для вѣчнаго удаленiя тѣлъ, брошенныхъ съ поверхности Марса или Меркурiя.

Если отношенiе массъ будетъ 3, то уже получится, по израсходованiи всего запаса, такая скорость снаряда, которой лишь немного не достаетъ для того, чтобы онъ могъ вращаться, за предѣлами атмосферы, вокругъ земли, подобно ея спутнику.

При отношенiи , равномъ 6, скорость ракеты почти достаточна для удаленiя ея отъ земли и вѣчнаго вращенiя вокругъ солнца въ качествъ самостоятельной планеты. При большемъ количествѣ взрывчатаго запаса, возможно достиженiе пояса Астероидовъ и даже тяжелыхъ планетъ.

Изъ таблицы видно, что и при небольшомъ запасѣ взрывчатыхъ веществъ, окончательная скорость снаряда еще достаточна для практическихъ цѣлей. Такъ при запасѣ, составляющемъ лишь 0,1 вѣса ракеты, скорость равна 543 метрамъ въ секунду, что довольно для поднятiя ракеты на 15 километровъ. Далѣе, изъ таблицы мы видимъ, что при незначительномъ запасѣ, скорость, по окончанiи взрыва, приблизительно, пропорцiональна мaccѣ запаса (M₂); слѣдовательно, въ этомъ случаѣ, высота поднятiя пропорциональна квадрату этой массы (М₂) запаса. Такъ, при заnacѣ составляющемъ половину массы ракеты =0,5, послѣдняя залетитъ далеко за предѣлы атмосферы.

Интересно определить, какая часть полной работы взрывчатыхъ веществъ, т. е. ихъ химической энергiи, передается ракетѣ

Работа взрывчатыхъ веществъ выразится , гдѣ (g) есть ycкоpeнie земной тяжести; механическая работа ракеты, имѣющей скорость (V) выразится въ тѣхъ же единицахъ: или на основанiи формулы 6:

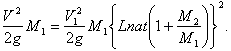
Раздѣливъ теперь работу ракеты на работу взрывчатаго матеpiaлa, получимъ:

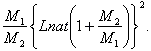
По этой формулѣ вычислимъ следующую таблицу утилизацiи ракетой энергiи взрывчатыхъ веществъ.

Изъ формулы и таблицы видно, что при очень малыхъ количествахъ взрывчатаго матерiала утилизацiя его равна отношенiю , т. е. тѣмъ меньше, чѣмъ относительное количество взрывчатыхъ веществъ меньше.

	Утили- зацiя		Утили- зацiя
0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6	0,090 0,165 0,223 0,282 0,328 0,480 0,600 0,64 0,65 0,64 0,63	7 8 9 10 19 20 30 50 100 193 Безконечно	0,62 0,60 0,59 0,58 0,47 0,46 0,39 0,31 0,21 0,144 Нуль

Далѣе, съ увеличенiемъ относительнаго количества взрывчатыхъ веществъ, утилизацiя возрастаетъ и, приблизительно при учетверенномъ ихъ количествѣ (сравнительно съ массой ракеты) достигаетъ наибольшей величины (0,65). Дальнѣйшее увеличенiе взрывчатыхъ веществъ, хотя и медленно, но непрерывно уменьшаетъ ихъ полезность; при безконечно-большомъ ихъ количествѣ, она нуль, также какъ и при безконечно-маломъ. Изъ таблицы также видимъ, что при измѣненiи отношенiя отъ 2 до 10, утилизацiя болѣе половины; это значитъ, что въ такомъ случаѣ болѣе половины потенцiальной энергiи взрывчатаго матерiала передается въ видѣ кинетической энергiи ракетѣ.

---

Ракета подъ влiянiемъ тяжести. Вертикальное поднятiе.

Мы опредѣлили скорость, прiобрѣтаемую ракетой въ пустотѣ и при отсутствiи силы тяготѣнiя, въ зависимости отъ массы ракеты, массы взрывчатыхъ веществъ и энергiи ихъ химическаго соединенiя.

Разберемъ теперь влiянiе постоянной силы тяжести на вертикальное движенiе снаряда.

Мы видѣли, что безъ влiянiя тяжести прiобрѣтаются ракетой огромныя скорости и утилизируется значительное количество энергiи взрыва. Это будетъ справедливо и для среды тяжести, если только взрывъ будетъ мгновенный. Но такой взрывъ для насъ не годится, потому что при этомъ получится убiйственный толчекъ, котораго не вынесетъ ни снарядъ, ни вещи и люди, заключенные въ немъ. Намъ, очевидно, нужно медленное взрыванiе; при медленномъ же взрыванiи полезный эффектъ уменьшается и даже можетъ обратиться въ нуль.

Дѣйствительно, пусть взрыванiе будетъ настолько слабо, что ycкоpeнie ракеты, происходящее отъ него, будетъ равно ускоренiю (g) земли. Тогда снарядъ, во все время взрыванiя, будетъ стоять въ воздухѣ неподвижно, безъ опоры.

Конечно онъ не прiобрѣтетъ при этомъ никакой скорости и утилiзацiя взрывчатыхъ веществъ, не смотря на ихъ количество, будетъ равняться нулю. Итакъ, крайне важно изследовать аналитически влiянiе на снарядъ тяготѣнiя.

Когда ракета двигается въ средѣ, свободной отъ силы тяжести, то время (t), въ теченiе котораго взрывается весь запасъ взрывчатаго вещества, равно:

7..., гдѣ (V) есть скорость снаряда по окончанiи взрыва, а (р) постоянное ускоренiе, сообщаемое ракетѣ взрывчатыми матерiалами въ 1 секунду времени.

Сила взрыванiя, т.е. количество веществъ, расходуемыхъ при взрывѣ въ единицу времени, въ этомъ простѣйшемъ случаѣ равномѣрно ускоряющагося движенiя снаряда, — не постоянна, но не прерывно ослабляется — пропорцiонально уменьшенiю массы снаряда съ остаткомъ невзорванныхъ матерiаловъ.

29. Зная (р), или ускоренiе въ средѣ безъ тяжести, можемъ выразить и величину кажущейся (временной) тяжести внутри ракеты въ теченiе ея ускоряющагося движенiя, или въ теченiе времени взрыванiя.

Принявъ силу тяжести у поверхности земли за единицу, найдемъ величину временной тяжести въ снарядѣ равной , гдѣ (g) есть земное ускоренiе; формула эта показываетъ, во сколько разъ давленiе на подставки всѣхъ вещей, помѣщенныхъ въ ракетѣ, больше давленiя тѣxъ жe вещей, лежащихъ на столѣ въ нашей комнатѣ при обыкновенныхъ условiяхъ. Весьма важно знать величину относительной тяжести въ снарядѣ, потому что она обусловливаетъ цѣлость или изломъ аппаратовъ и здоровье людей пустившихся въ путь для изученiя неизвѣстныхъ пространствъ и свойственныхъ имъ явленiй.

При влiянiи постоянной или перемѣнной тяжести, любой силы, время въ теченiе котораго расходуется одинъ и тотъ же запасъ взрывчатaro матерiала, будетъ то-же, как и безъ влiянiя тягoтѣнiя; оно выразится извѣстною намъ формулою (см. 7) или слѣдующею:

, гдѣ

(V₂) есть скорость ракеты по окончанiи взрыванiя въ средѣ тяжести съ постояннымъ ускоренiемъ (g); Тутъ, конечно, предполагается, что, (p) и (g) параллельны и противоположны (см. заглавiе главы); (р — g) выражаетъ видимое ускоренiе снаряда (относительно земли), являющееся результатомъ двухъ противоположныхъ силъ: силы взрыва и силы тяжести.

32. Дѣйствiе послѣдней на снарядъ нисколько не влiяетъ на относительную въ немъ тяжесть и она выражается безъ всякаго измѣненiя формулой 9.... Напр., если р=0, т.е. если взрыванiя нѣтъ, то нѣтъ и временной тяжести, потому что =0. Это значитъ, что если взрыванiе прекратится и снарядъ двигается въ ту или другую сторону только подъ влiянiемъ своей скорости и силы тяготѣнiя солнца, земли и другихъ звѣздъ и планетъ, то находящiйся въ снарядѣ наблюдатель ни самъ не будетъ имѣть, повидимому, ни малѣйшаго вѣса, — ни обнаружитъ его, при помощи самыхъ чувствительныхъ пружинныхъ вѣсовъ, ни въ одной изъ вещей, находящихся при немъ или въ ракетѣ. Падая или поднимаясь въ ней подъ влiянiемъ инерцiи даже у самой поверхности земли, наблюдатель не будетъ испытывать ни малѣйшей тяжести, пока, разумѣется, снарядъ не встрѣчаетъ никакихъ препятствiй, — въ видѣ, напр., сопротивленiя атмосферы, воды или твердаго грунта.

Если p=g, т. е. если давленiе взрывающихся газовъ равно тяжести снаряда (= 1), то относительная тяжесть будетъ равняться земной. Пpи начальной неподвижности, снарядъ въ этомъ случаѣ и остается неподвижнымъ во все время дѣйствiя взрыва; если же до него снарядъ имѣлъ какую нибудь скорость (вверхъ, въ бокъ, въ низъ), то эта скорость такъ и останется безъ всякаго измѣненiя, пока не израсходуется весь взрывчатый матерiалъ: тутъ тѣло, т. е. ракета уравновѣшена и двигается какъ бы по инерцiи въ средѣ, свободной отъ тяжести.

На основанiи формулъ 8 и получимъ:

Отсюда, зная какую скорость (V2) долженъ имѣть по окончанiи взрыва снарядъ, мы вычислимъ (V), по которой, съ помощiю формулы 6, опредѣлимъ и потребное количество (М2) взрывчатыхъ веществъ.

Изъ уравненiй 6 и 10 получимъ:

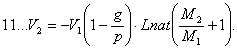
Изъ этой формулы, также какъ изъ предыдущей слѣдуетъ, что скорость, прiобрѣтаемая ракетой, меньше при влiянiи тяготѣнiя, чѣмъ безъ него (6). Она (V2) можетъ быть даже равна нулю не смотря на обилiе взрывчатаго запаса, если=1, т.е. если ускоpeнie, сообщаемое снаряду взрывчатымъ матерiаломъ, равно ускоренiю земной тяжести, или — давленiе газовъ равно и прямо противоположно дѣйствiю тяготѣнiя. (См. форм. 10 и 11).

Въ этомъ случаѣ ракета стоитъ нѣсколько минутъ неподвижно, нисколько не поднимаясь; когда же запасъ истощенъ, она падаетъ, какъ камень.

Чѣмъ больше (р) по отношенiю къ (g), тѣмъ большую скорость (V2) прiобрѣтаетъ снарядъ при данномъ количествѣ (M2) взрывчатыхъ веществъ (форм. 11).

Поэтому, желая подняться выше, надо сдѣлать (р) какъ можно больше, т. е, производить взрывъ какъ можно дѣятельнѣе. Однако, при этомъ, во-первыхъ, требуется болѣе крѣпкiй и массивный снарядъ, во-вторыхъ, — болѣе крѣпкiе предметы и аппарады въ снарядѣ, потому что (по 32) относительная тяжесть въ немъ будетъ весьма велика и въ особенности опасна для живого наблюдателя, если таковый отправляется въ ракетѣ.

Во всякомъ случаѣ, на основанiи формулы 11-ой, въ предѣлѣ,

т. е., если (р) безконечно велико, или взрывъ моменталенъ, то скорость, (V2) ракеты въ средѣ тяжести та-же что и въ средѣ безъ тяжести.

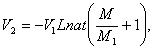
Согласно формулѣ 8 время взрыванiя не зависитъ отъ силы тяготѣния, а лишь исключительно отъ количества взрывчатаго матepiaлa и быстроты ихъ взрыванiя (р).

39. Любопытно опредѣлить эту величину. Положимъ въ форм. 7  V=11.100 метровъ (см. таблицу), a p=g=9,8 метра; тогда t = 1.133 секунды.

Значитъ въ средѣ, свободной отъ тяжести, ракета пролетѣла равномерно ускоряющимся движенiемъ менѣе 19 минутъ — и это при ушестеренномъ количествѣ взрывчатыхъ веществъ сравнительно съ массою снаряда (см. табл.).

При взрыванiи-же у поверхности нaшeй планеты, онъ простоялъ бы неподвижно въ теченiи тѣхъ-же 19 минутъ.

40. Если =1, то, по табл. V=3.920 метровъ; слѣдовательно, t=400 секундамъ, или 6²/₃ минуты.

При = 0,1, V=543 метра, a t = 55,4 секунды, т. е. менѣе минуты. Въ послѣднемъ случаѣ, у поверхности земли, снарядъ простоялъ бы неподвижно 55½ секундъ.

Отсюда мы видимъ, что взрыванiе у поверхности планеты, или вообще въ средѣ, несвободной отъ силы тяжести, можетъ быть совершенно безрезультатнымъ, если происходитъ, хотя и долгое время, но съ недостаточною силою: дѣйствительно, сиарядъ остается на мѣстѣ и не получаетъ никакой поступательной скорости, если не прiобрѣлъ ее раньше; въ противномъ случаѣ, онъ можетъ совершить нѣкоторое перемѣщенiе съ равномѣрною скоростью. Если это перемѣщенiе совершается въ верхъ, то снарядъ сдѣлаетъ нѣкоторую работу. Въ случаѣ первоначальной горизонтальной скорости и перемѣщенiе будетъ горизонтально; работы тутъ не будетъ, но тогда снарядъ можетъ служить для такихъ-же цѣлей, какъ локомотивъ, пароходъ, или управляемый аэростатъ. Служить для этихъ цѣлей перемѣщенiя снарядъ можетъ только въ теченiе нѣсколькихъ минутъ, пока совершается взрыванiе, но и въ такое небольшое время онъ можетъ пройти значительное пространство.

Время стоянiя прибора въ средѣ тяготѣнiя обратно пропорцiонально (g), т. е. силѣ этого тяготѣнiя.

Такъ на лунѣ приборъ простоялъ бы неподвижно безъ опоры (при = 6) въ теченiе 2 часовъ.

А. Положимъ въ формулѣ 8, для среды съ тяжестью: =10; =6; тогда вычислимъ V2 = — 9990 метровъ. Относительная тяжесть, по предыдущаго будетъ равна 10, т. е. человѣкъ въ 70 килограммовъ вѣcoмъ, во все время взрыванiя (около 2 минутъ) будетъ испытывать тяжесть въ 10 разъ большую, чѣмъ на землѣ и будетъ вѣсить на пружинныхъ вѣсахъ 700 килограммовъ (пудовъ 40). Такую тяжесть путешественникъ можетъ перенести безъ вреда только при соблюденiи особыхъ предосторожностей: при погруженiи въ особую жидкость при особенныхъ условiяхъ.

На основанiи формулы на стр. 60, вычислимъ и время взрыванiя, или время этой усиленной тяжести; получимъ 113 секундъ, т.е. менѣе двухъ минуть. Это очень немного и кажется съ перваго раза поразительнымъ, какъ можетъ снарядъ въ теченiе такого ничтожнаго промежутка времени прiобрѣсти скорость, чуть недостаточную для удаленiя отъ земли и движенiя вокругъ солнца подобно новой планетѣ.

Мы нашли V2= — 9990 метровъ, т. е. такую скорость, которая лишь немного менѣе скорости (V), прiобрѣтаемой въ средѣ свободной отъ силы тяготѣнiя, при тѣхъ же условiяхъ взрыва (см. табл. I). Но такъ какъ снарядъ во время взрыванiя еще и поднимается на некоторую высоту, то приходитъ даже въ голову, что общая работа взрывчатыхъ веществъ совсѣмъ не уменьшилась сравнительно съ работою ихъ въ средѣ безъ тяжести. Вопросъ этотъ мы сейчасъ разберемъ.

Уcкopенiе снаряда въ средѣ тяжести выразится р1 = р — g.

На разстоянiи отъ поверхности земли, не превышающемъ нѣсколькихъ сотенъ версть, мы (g) примемъ постояннымъ, что не повлечетъ за собой большой погрѣшности; да и погрѣшность то будетъ въ неблагопрiятную сторону, т. е. истинныя числа будутъ благопрiятнѣе для полета, чѣмъ вычисленныя нами.

Высота (h) поднятiя снаряда, во время (t) дѣйствiя взрыва, будетъ.

выключая отсюда (t), по уравненiю 31, получимъ: , гдѣ (V2) есть скорость снаряда въ средѣ тяжести, по истощенiи всего взрывчатаго запаса.

Теперь получимъ, выключая (V2):

гдѣ (V) есть скорость, прiобрѣтаемая ракетой въ средѣ, свободной отъ тяготѣнiя. Полезная работа взрывчатыхъ веществъ въ такой средѣ выразится: Работа же (T1) въ средѣ тяжести выразится въ зависимости отъ высоты поднятiя снаряда и его скорости по окончанiи взрыва; именно: Отношенiе этой работы къ предыдущей, идеальной, равно: Исключивъ отсюда (h) и (V) найдемъ: т. е. работа въ средѣ тяготѣнiя, получаемая отъ опредѣленнаго количества взрывчатыхъ веществъ (М2), менѣе, чѣмъ въ средѣ свободной отъ него; разница эта тѣмъ меньше, чѣмъ быстрѣе взрываются газы, или чѣмъ болѣе (р). Напр., въ случаѣ А (стр. 65), потеря составляетъ только 1/10, а утилизацiя (18) равна 0,9. Когда p=g, или когда снарядъ стоитъ въ воздухѣ, не имѣя даже постоянной скорости, потеря будетъ полная (1), а утилизация равна нулю. Такова же будетъ утилизацiя, если снарядъ имѣет постоянную горизонтальную скорость.

Въ парагр. А мы вычислили V₂=9990 мотровъ. Примѣнимъ формулу 13 къ случаю А найдемъ: h=565 километровъ; значитъ, въ теченiи взрыва, снарядъ зайдетъ далеко за пределы атмосферы и прiобрѣтетъ еще поступательную cкopость в 9990 метровъ.

Замѣтимъ, что скорость эта на 1.110 метровъ меньше, чѣмъ въ средѣ, свободной отъ силы тяготѣнiя. Эта разность составляетъ какъ разъ 1/10 скорости въ средѣ безъ тяжести (см. табл. 22).

Отсюда видно, что потеря въ скорости подчиняется тому же закону, какъ и потеря работы (см. 51), что, впрочемъ, строго слѣдуетъ и изъ формулы 34, преобразуя которую, получимъ:

Найдемъ:

гдѣ (Т1) есть работа, получаемая снарядомъ отъ взрывчатыхъ веществъ въ средѣ тяготѣнiя, сила которого равна (g).

Чтобы снарядъ могъ совершить всѣ необходимые работы, поднимаясь въ высоту, преодолѣвая сопротивленiе атмосферы и прiобрѣтая желаемую скорость, — необходимо, чтобы сумма всѣхъ этихъ работъ равнялась (T1).

Опредѣливъ всѣ эти работы, съ помощiю формулы 56, вычислимъ Т. Зная же (Т), вычислимъ и (V), т. е. скорость въ средѣ безъ тяжести, по формулѣ:

Зная теперь (V), можемъ разсчитать и потребную массу (М₂) взрывчатыхъ веществ по формулѣ 16.

Такимъ путемъ, съ помощiю предыдущаго, найдемъ:

20... M2=M₁ Вычисляя, мы заменили для краткости черезъ (Т2).

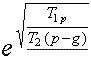
Итакъ, зная массу снаряда M₁ со всѣмъ содержимымъ кромѣ взрывчатаго матерiала (М₂), механическую работу (Т2) взрывчатыхъ веществъ при массѣ ихъ, равной массѣ снаряда (M₁) работу (Т), которую долженъ совершить снарядъ при своемъ вертикальномъ поднятiи, силу взрыванiя (р) и силу тяготения (g), — можемъ узнать и количество взрывчатыхъ веществъ (М₂), необходимое для поднятiя массы (M₁) снаряда.

Отношение въ формулѣ не измѣнится, если его сократить на (M₁). Такъ что подъ (T1) и (Т2) можно подразумевать механическую работу (T1), совершаемую единицею массы снаряда и механическую работу (Т2) единицы взрывчатыхъ веществъ.

Подъ (g) нужно, вообще, подразумевать постоянное сопротивленiе, равное суммѣ силъ тяжести и сопротивленiя среды. Но сила тяготѣния постепенно убываетъ съ удаленiемъ отъ центра земли, вслѣдствiе чего утилизируется большее количество механической работы взрывчатыхъ веществъ. Съ другой стороны, сопротивленiе атмосферы, будучи, какъ увидимъ, сравнительно съ тяжестью снаряда, весьма незначительнымъ, — уменьшаетъ утилизацiю энергiи взрывчатыхъ веществъ.

По нѣкоторомъ размышленiи увидимъ, что послѣдняя убыль, продолжаясь недолгое время пролета черезъ воздухъ, съ избыткомъ вознаграждается прибылью отъ уменьшенiя притяженiя на разстоянiяхъ значительныхъ (500 килом.), гдѣ кончается дѣйствiе взрывчатыхъ веществъ.

Итакъ, формулу 20 можемъ смѣло примѣнять къ вертикальному поднятiю снаряда, несмотря на осложненiе отъ измѣненiя тяжести и сопротивленiя атмосферы (g=9,8 метровъ).

---

Среда тяжести. Отвѣсное возвращенiе на землю.

Разсмотримъ сначала остановку въ средѣ, свободной отъ тяжести или моментальную остановку въ средѣ тяжести. Пусть, напр., ракета силою взрыва нѣкоторого (не всего) количества газовъ прiобрѣла скорость 10.000 метровъ въ секунду (см. табл. 22). Теперь, для остановки, слѣдуетъ прiобрѣсти такую же скорость, но въ обратномъ направленiи. Очевидно, количество оставшихся взрывчатыхъ веществъ, согласно таблицѣ I, должно быть въ 5 разъ больше массы (M₁) снаряда. Стало-быть снарядъ долженъ имѣть, по окончанiи первой части взрыва (для прiобрѣтенiя поступательной скорости), запасъ взрывчатаго вещества, масса котораго выразится через 5 M₁ = М₂.

Вся масса, вмѣстѣ съ запасомъ, составитъ М₂ + М₁ = 5 М₁ + М₁ = 6 M₁.

Этой массѣ (6M₁) первоначальное взpыванie должно также сообщить скорость въ 10.000 метровъ, а для этого нужно новое количество взрывчатаго матерiала, которое должно также въ 5 разъ (см. 22) превышать массу снаряда съ массою запаса для остановки; т. е. мы должны ее (6M₁) увеличить въ 5 разъ; получимъ 30M₁, что вмѣстѣ съ запасомъ для остановки (5M₁) составитъ 35M₁.

Означивъ число табл. I, показывающее во сколько разъ масса взрывчатаго матерiала больше массы снаряда, черезъ (q) , предыдущiя рассужденiя, опредѣляющiя массу всего взрывчатаго вещества для прiобрѣтенiя скорости и уничтоженiя ея, выразимъ такъ:

21. =q+(1+q)· q = q (2+q), или прибавляя и вычитая единицу изъ второй части уравненiя, получимъ: 22. = 1+2 q+q² = (1 — q)² — 1.

Всего же, съ массою ракеты (M₁, или 1) найдемъ: + 1 = (1 + q) ². Последнее выраженiе легко запомнить.

Когда (q) очень мало, то, приблизительно, количество взрывчатаго вещества равно 2 q (потому что (q² будетъ ничтожно), т. е. оно только вдвое больше; чѣмъ для одного прiобрѣтенiя скорости.

На основанiи полученныхъ формулъ таблицы I, составимъ слѣдующую таблицу:

Табл. II. Въ средѣ безъ тяжести.

V. Метры.	M2:M1.	M3:M1	V. Метры.	M2:M1.	M3:M1
543 1.037 1.493 1.915 2.308 3.920 6.260 7.880 9.170 10.100 11.100	0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6	0,21 0,44 0,69 0,96 2,25 3 8 15 24 35 48	11.800 12.500 13.100 13.650 17.100 17.330 19.560 22.400 26.280 30.038 Безконечно.	7 8 9 10 19 20 30 50 100 193	63 80 99 120 399 440 960 2.600 10.200 37.248 Безконечно.

Изъ нея видимъ, какъ неодолимо громаденъ запасъ взрывчатаго матерiала, если мы хотимъ прiобрѣсти очень большую скорорость и потерять ее.

Эту таблицу можемъ составить и посредствомъ формулы 6, изъ которой имѣемъ:

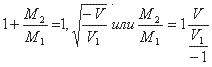
Замѣтимъ, что отношенiе, положительно, потому что скорости снаряда и газовъ противоположны по направленiю и слѣдовательно имѣютъ разные знаки.

Полагая въ послѣдней формулѣ (V) вдвое большимъ, чѣмъ въ первомъ столбцѣ таблицы, получимъ отношенiе т. е. относительное количество взрывчатаго матерiала, потребное для прiобрѣтенiя скоростей послѣдней таблицы и послѣдующаго уничтоженiя ихъ.

Если мы находимся въ средѣ тяжести, то въ простѣйшемъ случаѣ вертикальнаго движенiя процессъ остановки и опусканiя на землю будетъ такой: когда ракета, подъ влiянiемъ прiобрѣтенной скорости поднялась на известную высоту и остановилась, то начинается ея паденiе на землю. Когда снарядъ достигнетъ той точки, въ которой окончилось при поднятiи дѣйствiе взрывчатыхъ веществъ, онъ снова подвергается влiянiю остатка ихъ, — въ томъ же направленiи и въ томъ же порядкѣ. Очевидно, къ концу ихъ дѣйствiя и истощенiя всего запаса, ракета остановится въ той точкѣ, у поверхности земли, съ которой было начато поднятiе. Способъ поднятiя строго тождественъ со способомъ опусканiя; вся разница лишь въ томъ, что скорости обратны въ каждой точкѣ пути.

Остановка въ средѣ тяжести требуетъ болѣе работы и болѣе взрывчатыхъ веществъ чѣмъ въ средѣ свободной отъ тяготѣнiя; потому что въ формулахъ 21 и 22 (q) должно быть больше, если примѣнять ракету къ средѣ тяжести.

Обозначивъ это большое отношенiе черезъ (q₁), найдемъ на основанiи предыдущаго:

, откуда

Подставивъ (q1) вмѣсто (q) въ уравненiе 22, получимъ.

23...q=q1

Здѣсь (М4) означаетъ количество, или массу взрывчатыхъ веществ, необходимую для поднятiя съ известной точки и возращенiя въ ту-же точку при полной остановкѣ ракеты и при полетѣ ея въ средѣ тяжести.

На основанiи послѣдней формулы можемъ составить следующую таблицу, полагая, что =10, т. е., что давленiе взрывчатаго матерiала въ 10 разъ больше тяжести ракеты съ остаткомъ взрывчатыхъ веществъ. Въ этой таблицѣ (V) выражаетъ собственно работу ; — скорость же будетъ меньше, потому что часть этой работы ушла на поднятiе въ средѣ тяжести.

Табл. III. Для среды тяжести.

V в метр. 543 1.497 2.308 3.920 6.260 7.880 9.170 10.100 11.100 11.800

M2:M1 0,1 0,3 0,5 1,0 2 3 4 5 6 7

M4:M1 0,235 0,778 1,420 4,457 9,383 17,78 28,64 41,98 57,78 76,05

---

Среда тяжести. Наклонное поднятie.

Хотя вертикальное движенiе ракеты какъ будто выгоднѣе, потому что при этомъ cкopѣе разсѣкается атмосфера и снарядъ подымается на большую высоту; — но, съ одной стороны, работа разсѣченiя атмосферы, сравнительно съ полною работою взрывчатыхъ веществъ, весьма незначительна, съ другой, при наклонномъ движенiи, можно устроить постоянную обсерваторiю, движущуюся за пределами атмосферы неопредѣленно долгое время вокругъ земли, подобно ея лунѣ. Кромѣ того и это главное — при наклонномъ полетѣ утилизируется несравненно большая часть энергiи взрыва, чѣмъ при вертикальномъ движенiи.

Разсмотримъ сначала частный случай, — когда полетъ ракеты горизонталенъ.

Если черезъ (R) обозначимъ величину равнодействующей горизонтальнаго ycкopенiя ракеты, черезъ (р) ускоренiе отъ дѣйствiя взрыванiя и черезъ (g) ycкopeнie отъ силы тяжести, то имѣемъ:

Кинетическая энергiя, полученная снарядомъ чрезъ время (t), равна, на основанiи послѣдней формулы:

гдѣ (t) есть время взрыванiя. Это и есть вся полезная работа, прiобрѣтенная ракетой. Действительно ракета нисколько не поднимется, если принять направленiе тяжести постояннымъ (что на практикѣ только при небольшой траекторiи снаряда вѣрно).

Работа-же взрывчатыхъ веществъ, прiобрѣтенная ракетой въ средѣ, свободной отъ тяжести, равна:

Разделив полезную работу (25) на полную (26), получимъ утилизацiю при горизонтальномъ полетѣ ракеты:

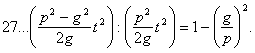
Сопротивленiе воздуха, какъ и прежде, пока въ расчетъ не принимается.

Изъ послѣдней формулы видно, что потеря работы, сравнительно съ работою въ средѣ, свободной отъ силы тяготѣнiя, выражается черезъ Отсюда слѣдуетъ, что эта потеря гораздо меньше, чѣмъ при отвѣсномъ движенiи. Такъ напр., при потеря составитъ 1/100 т. е. одинъ процентъ между тѣмъ какъ при вертикальномъ движенiи она выражалась черезъ или равнялась 1/10 т. е. десяти процентамъ.

Вотъ таблiца, гдѣ (В) есть уголъ наклоненiя силы (р) къ горизонту:

Горизонтальное движенiе ракеты.

p:g 1 2 3 4 5 10 100

Потеря 1 1:4 1:9 1:16 1:25 1:100 1:10 000

sin β 1 1:2 1:3 1:4 1:5 1:10 1:100

β Градусы 90° 30 19,5 14,5 11,5 5,7 0,57

Теперь рѣшимъ вопросъ вообще, — при всякомъ наклоненiи равнодѣйствующей (В). Горизонтальность траекторiи, или равнодѣйствующей, какъ я уже говорилъ, невыгодна потому, что при такомъ движенiи снаряда страшно увеличивается его путь черезъ атмосферу, a вмѣстѣ съ тѣмъ увеличивается и работа разсѣченiя имъ воздуха.

Итакъ, будемъ помнить, что (α), или уголъ наклоненiя равнодѣйcтвyющей къ вертикали, больше прямого угла, Имѣемъ:

гдѣ (γ)= α+3 (тyпoй уголъ параллелограмма, по чертежу ). Далѣе: sin (α): sin (β): sin (γ) = р:g R1 и

Кинетическая работа выражается формулой 9, гдѣ (R) опредѣляется согласно ypавненiю 29. Вертикальное ускоренiе (R1) равнодѣйствующей (R) равно; 79...R1=sin (α-90). R= -cos (α).R.

Слѣдовательно работа поднятiя снаряда будетъ равна:

гдѣ (t) есть время взрыванiя всего запаса взрывчатыхъ веществъ. Полная работа, прiобрѣтенная снарядомъ съ средѣ тяжести, выразится:

Здѣсь за единiцу работы принято поднятiе снаряда на единицу высоты, въ средѣ съ ускоренiемъ (g). Если [α] 90°, напр. въ случаѣ поднятiя снаряда, то (- cos α) есть величина положiтельная и обратно.

Работа въ средѣ, свободной отъ тяжести, будетъ, равна.

(не забудемъ, что время (t) взрыванiя не зависитъ отъ силъ тяготѣнiя).

Взявъ отношенiе этихъ двухъ работъ получимъ утилизацiю энергiи взрывчатыхъ веществъ, сравнительно съ утилизацiею ихъ въ средѣ лишенной тяжести; именно:

Выключая отсюда (R) по формулѣ 29, найдемъ:

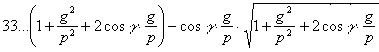
Формула 27 напр. есть только частный случай этой, въ чемъ легко убѣдиться.

Сдѣлаемъ сейчасъ же примѣненiе найденной формулы. Положимъ, что ракета летитъ въ верхъ подъ угломъ въ 14,5° къ горизонту; синусъ этого угла составляетъ 0,25; это значитъ, что сопротивленiе атмосферы увеличивается въ 4 раза сравнительно съ сопротивленiемъ ея при отвѣсномъ движенiи снаряда; ибо, приблизительно, сопротивленiе ея обратно пропорцiонально синусy угла наклона (α — 90°) траекторiи ракеты къ горизонту.

85. Уголъ α = 90 + 14½ = 104½ °; соs α = — 0,25; зная (α), можемъ узнать и (β); дѣйствительно, найдем: sin β = sin α·; такъ, если = 0,1, то sin β = 0,0968, откуда β = 110°; cos γ = — 0,342.

Теперь, пo формулѣ 32, вычислимъ отилизацiю въ 0,966. Потеря составляетъ 0,034, или около 1/29,вѣрнѣе, 3,4%.

Эта потеря въ 3 раза меньше, чѣмъ при вертикальномъ движенiи. Результатъ недурной, если прнять еще во вниманiе, что сопротивленiе атмосферы и при наклонномъ движенiи (14½ °) , никакъ не болѣе одного процента работы удаленiя снаряда отъ земли.

Для разныхъ соображенiй предлагаемъ слѣдующую таблицу. 1-й столбецъ показываетъ наклоненiе движенiя къ горизонту, послѣднiй потерю работы; (β) есть отклоненiе направленiя давленiя взрывчатыхъ веществъ отъ линiи дѣйствительнаго движенiя

Наклонное движенiе.

Градусы				утилизацiя	Потеря.
α — 90. 0 2 5 10 15 20 30 40 45 90	α. 90 92 95 100 105 110 120 130 135 180	β. 53/4 52/3 52/3 52/3 51/2 51/3 5 41/3 4 0	γ = α+β 952/3 972/3 1002/3 1052/3 1101/2 1151/3 125 1341/3 139 180	0,9900 0,9860 0,9800 0,9731 0,9651 0,9573 0,9426 0,9300 0,9246 0,9000	1:100 1:72 1:53 1:37 1:29 1:23,4 1:17,4 1:14,3 1:13,3 1:10

Для очень малыхъ угловъ наклона (α — 90°), формулу 33 можно чрезвычайно упростить, замѣнивъ тригонометрическiя величины ихъ дугами и сдѣлавъ другiя упрощенiя.

Тогда получимъ следующее выраженiе для потери работы:

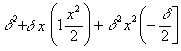гдѣ (δ) означаетъ уголъ наклона движенiя (α — 90°), выраженный длиною его дуги, радiусъ который равенъ единицѣ, — а (х) — отношенiе

Откидывая въ последней формулѣ малыя высшихъ порядковъ, получимъ для потери:

Можемъ положить.

δ = 0,02N, гдѣ 0,02 есть часть окружности, соотвѣтствующая почти одному градусу a (N) число этихъ новыхъ градусовъ. Таким образомъ потеря работы, приблизительно выразится;

По этой формулѣ легко составимъ следующую таблицу, положивъ =0,1

N	0	0,5	1	2	3	4	5	6	10
Потеря	1/100	1/91	1/83	1/70	1/60	1/55	1/50	1/45	1/33

Отсюда видимъ, что даже для большихъ угловъ (до 10°) противоречие между этой таблицой и предыдущей, болѣе точной, не велико.

---

Мы могли бы разсмотрѣть еще очень многое: работу тяготѣнiя, сопротивленiе атмосферы; мы совсѣмъ еще ничего не сказали о томъ какъ изслѣдователь можетъ пробыть продолжительное, даже неопределенно долгое время въ средѣ, гдѣ нѣтъ слѣдовъ кислорода; мы не упомянули о нагрѣванiи снаряда при кратковременномъ полетѣ въ воздухѣ, мы не дали даже общей картины полета и сопровождающихъ его крайне интересныхъ явленiй (теоретически); мы почти не указали на великiя перспективы въ случаѣ осуществленiя дѣла, рисущiяся намъ пока еще въ туманѣ наконецъ, мы могли-бы начертать космическiя кривыя движенiя ракеты въ небесномъ пространствѣ.